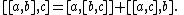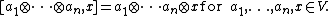- Notes
- References
In mathematics, a (right) Leibniz algebra, named after Gottfried Wilhelm Leibniz, sometimes called a Loday algebra, after Jean-Louis Loday, is a module L over a commutative ring R with a bilinear product [ _ , _ ] satisfying the Leibniz identity
In other words, right multiplication by any element c is a derivation. If in addition the bracket is alternating ([a, a] = 0) then the Leibniz algebra is a Lie algebra. Indeed, in this case [a, b] = −[b, a] and the Leibniz's identity is equivalent to Jacobi's identity ([a, [b, c]] + [c, [a, b]] + [b, [c, a]] = 0). Conversely any Lie algebra is obviously a Leibniz algebra.
In this sense, Leibniz algebras can be seen as a non-commutative generalization of Lie algebras. The investigation of which theorems and properties of Lie algebras are still valid for
Leibniz algebras is a recurrent theme in the literature.[1] For instance, it has been shown that Engel's theorem still holds for Leibniz algebras[2][3] and that a weaker version of Levi-Malcev theorem also holds.[4]
The tensor module, T(V) , of any vector space V can be turned into a Loday algebra such that
This is the free Loday algebra over V.
Leibniz algebras were discovered in 1965 by A. Bloh, who called them D-algebras. They attracted interest after Jean-Louis Loday noticed that the classical Chevalley–Eilenberg boundary map in the exterior module of a Lie algebra can be lifted to the tensor module which yields a new chain complex. In fact this complex is well-defined for any Leibniz algebra. The homology HL(L) of this chain complex is known as Leibniz homology. If L is the Lie algebra of (infinite) matrices over an associative R-algebra A then Leibniz homology
of L is the tensor algebra over the Hochschild homology of A.
A Zinbiel algebra is the Koszul dual concept to a Leibniz algebra. It has defining identity:
Notes
2. ^{{cite journal|last1=Patsourakos|first1=Alexandros|title=On Nilpotent Properties of Leibniz Algebras|journal=Communications in Algebra|date=26 November 2007|volume=35|issue=12|pages=3828–3834|doi=10.1080/00927870701509099}}
3. ^{{cite book|author1=Sh. A. Ayupov|author2=B. A. Omirov|editor1-last=Khakimdjanov|editor1-first=Y.|editor2-last=Goze|editor2-first=M.|editor3-last=Ayupov|editor3-first=Sh.|title=Algebra and Operator Theory Proceedings of the Colloquium in Tashkent, 1997|date=1998|publisher=Springer|location=Dordrecht|isbn=9789401150729|pages=1–13|chapter=On Leibniz Algebras}}
4. ^{{cite journal|last1=Barnes|first1=Donald W.|title=On Levi's theorem for Leibniz algebras|journal=Bulletin of the Australian Mathematical Society|date=30 November 2011|volume=86|issue=2|pages=184–185|doi=10.1017/s0004972711002954|arxiv=1109.1060}}
References
- {{cite journal | first= Yvette| last=Kosmann-Schwarzbach | authorlink = Yvette Kosmann-Schwarzbach | title= From Poisson algebras to Gerstenhaber algebras | journal= Annales de l'Institut Fourier | year=1996 | url= | doi= 10.5802/aif.1547| volume= 46| issue = 5 | pages= 1243–1274 }}
- {{cite journal | first=Jean-Louis | last=Loday | title= Une version non commutative des algèbres de Lie: les algèbres de Leibniz | journal= Enseign. Math. (2) | year=1993 | url= | doi= | volume= 39| issue = 3–4 | pages= 269–293 }}
- {{Cite journal |doi=10.1007/BF01445099 |last=Loday |first=Jean-Louis |lastauthoramp=yes |first2=Pirashvili |last2=Teimuraz |year=1993 |title=Universal enveloping algebras of Leibniz algebras and (co)homology |journal=Mathematische Annalen |volume=296 |issue= 1|pages=139–158 |citeseerx=10.1.1.298.1142 }}
- {{Cite journal | first= A. | last=Bloh | title= On a generalization of the concept of Lie algebra | journal= Dokl. Akad. Nauk SSSR | year= 1965 | url= | doi= | volume=165 |issue= | pages=471–473 }}
- {{Cite journal | first= A. | last=Bloh | title= Cartan-Eilenberg homology theory for a generalized class of Lie algebras | journal= Dokl. Akad. Nauk SSSR | year= 1967 | url= | doi= | volume= 175 |issue= 8| pages=824–826 }}
- {{cite journal | first1=A.S. | last1=Dzhumadil'daev | first2=K.M. | last2=Tulenbaev | title=Nilpotency of Zinbiel algebras | journal=J. Dyn. Control Syst. | volume=11 | number=2 | year=2005 | pages=195–213 | doi=10.1007/s10883-005-4170-1 }}
- {{cite journal | first1=V. | last1=Ginzburg | authorlink=Victor Ginzburg | first2=M. | last2=Kapranov | title=Koszul duality for operads | journal=Duke Math. J. | volume=76 | year=1994 | pages=203–273 | arxiv=0709.1228 | doi=10.1215/s0012-7094-94-07608-4}}