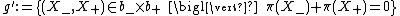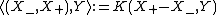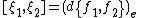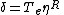“Lie bialgebra”的意思、由来-开放百科全书

词条

Lie bialgebra

释义

Definition
Example
Relation to Poisson-Lie groups
See also
References

In mathematics, a Lie bialgebra is the Lie-theoretic case of a bialgebra: it's a set with a Lie algebra and a Lie coalgebra structure which are compatible.

It is a bialgebra where the comultiplication is skew-symmetric and satisfies a dual Jacobi identity, so that the dual vector space is a Lie algebra, whereas the comultiplication is a 1-cocycle, so that the multiplication and comultiplication are compatible. The cocycle condition implies that, in practice, one studies only classes of bialgebras that are cohomologous to a Lie bialgebra on a coboundary.

They are also called Poisson-Hopf algebras, and are the Lie algebra of a Poisson-Lie group.

Lie bialgebras occur naturally in the study of the Yang-Baxter equations.

Definition

A vector space is a Lie bialgebra if it is a Lie algebra,

and there is the structure of Lie algebra also on the dual vector space 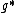which is compatible.

More precisely the Lie algebra structure on is given

by a Lie bracket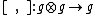

and the Lie algebra structure on 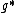is given by a Lie

bracket .

Then the map dual to is called the cocommutator,

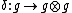
and the compatibility condition is the following cocycle relation:

where 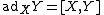is the adjoint.

Note that this definition is symmetric and 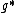is also a Lie bialgebra, the dual Lie bialgebra.

Example

Let be any semisimple Lie algebra.

To specify a Lie bialgebra structure we{{Who?|Wikipedia is an encyclopedia, not an algebra textbook|date=April 2019}} thus need to specify a compatible Lie algebra structure on the dual vector space.

Choose a Cartan subalgebra and a choice of positive roots.

Let be the corresponding opposite Borel subalgebras, so that and there is a natural projection .

Then define a Lie algebra

which is a subalgebra of the product , and has the same dimension as .

Now identify with dual of via the pairing

where and is the Killing form.

This defines a Lie bialgebra structure on , and is the "standard" example: it underlies the Drinfeld-Jimbo quantum group.

Note that is solvable, whereas is semisimple.

Relation to Poisson-Lie groups

The Lie algebra of a Poisson-Lie group G has a natural structure of Lie bialgebra.

In brief the Lie group structure gives the Lie bracket on as usual, and the linearisation of the Poisson structure on G

gives the Lie bracket on

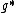(recalling that a linear Poisson structure on a vector space is the same thing as a Lie bracket on the dual vector space).

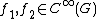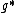In more detail, let G be a Poisson-Lie group, with being two smooth functions on the group manifold. Let be the differential at the identity element. Clearly, . The Poisson structure on the group then induces a bracket on , as

where 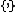is the Poisson bracket. Given be the Poisson bivector on the manifold, define to be the right-translate of the bivector to the identity element in G. Then one has that

The cocommutator is then the tangent map:

so that

is the dual of the cocommutator.

References

H.-D. Doebner, J.-D. Hennig, eds, Quantum groups, Proceedings of the 8th International Workshop on Mathematical Physics, Arnold Sommerfeld Institute, Claausthal, FRG, 1989, Springer-Verlag Berlin, {{isbn|3-540-53503-9}}.
Vyjayanthi Chari and Andrew Pressley, A Guide to Quantum Groups, (1994), Cambridge University Press, Cambridge {{isbn|0-521-55884-0}}.
{{cite journal | last1 = Beisert | first1 = N. | last2 = Spill | first2 = F. | year = 2009 | title = The classical r-matrix of AdS/CFT and its Lie bialgebra structure | url = | journal = Communications in Mathematical Physics | volume = 285 | issue = 2| pages = 537–565 | doi = 10.1007/s00220-008-0578-2 | arxiv = 0708.1762 | bibcode = 2009CMaPh.285..537B }}

3 : Lie algebras|Coalgebras|Symplectic geometry

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Definition

Example

Relation to Poisson-Lie groups

See also

References