- Statement of the theorem
- Proof
- References
In mathematics, Lindelöf's theorem is a result in complex analysis named after the Finnish mathematician Ernst Leonard Lindelöf. It states that a holomorphic function on a half-strip in the complex plane that is bounded on the boundary of the strip and does not grow "too fast" in the unbounded direction of the strip must remain bounded on the whole strip. The result is useful in the study of the Riemann zeta function, and is a special case of the Phragmén–Lindelöf principle. Also, see Hadamard three-lines theorem.
Statement of the theorem
Let Ω be a half-strip in the complex plane:
Suppose that ƒ is holomorphic (i.e. analytic) on Ω and that there are constants M, A and B such that
and
Then f is bounded by M on all of Ω:
Proof
Fix a point 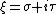 inside
inside  . Choose
. Choose  , an integer
, an integer 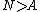 and
and  large enough such that
large enough such that
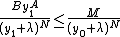 . Applying maximum modulus principle to the function
. Applying maximum modulus principle to the function 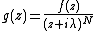 and
and
the rectangular area  we obtain
we obtain  , that is,
, that is, 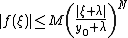 . Letting
. Letting  yields
yields
 as required.
as required.
References
- {{cite book|author=Edwards, H.M.|authorlink=Harold Edwards (mathematician)|title=Riemann's Zeta Function|publisher=Dover|location=New York, NY|year=2001|isbn=0-486-41740-9}}
- China-Myanmar border
- China-Myanmar relations
- China-Namibia relations
- China (nation)
- China National Agrochemical Corporation
- China National Aviation Company Limited
- China National Aviation Fuel
- China National Aviation Fuel Group
- China National Aviation Fuel Group Corporation
- China National Aviation Fuel Supply
- China National Aviation Holding
- China national B football team
- China National Biotech Group
- China National Building Material Company
- China National Building Material Group
- China National Center for the Performing Arts Orchestra
- China National Chemical Engineering Group
- China National Coal Group Corporation
- China National Electronics Import & Export Corporation
- China National Erzhong Group
- China national football B team
- China national football team head to head
- China national football team kit
- China national football team kit history
- China national football team kits



