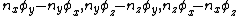1. Form

2. Examples

3. Symmetry
     Odd case    Even case    Consequences  

4. References

In knot theory, a Lissajous knot is a knot defined by parametric equations of the form

where 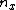, , and are integers and the phase shifts , , 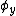and may be any real numbers.^[1]

The projection of a Lissajous knot onto any of the three coordinate planes is a Lissajous curve, and many of the properties of these knots are closely related to properties of Lissajous curves.

Replacing the cosine function in the parametrization by a triangle wave transforms every Lissajous

knot isotopically into a billiard curve inside a cube, the simplest case of so-called billiard knots.

Billiard knots can also be studied in other domains, for instance in a cylinder.^[2]

Form

Because a knot cannot be self-intersecting, the three integers must be pairwise relatively prime, and none of the quantities

may be an integer multiple of pi. Moreover, by making a substitution of the form , one may assume that any of the three phase shifts , , 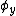is equal to zero.

Examples

Here are some examples of Lissajous knots,^[3] all of which have :

There are infinitely many different Lissajous knots,^[4] and other examples with 10 or fewer crossings include the 7₄ knot, the 8₁₅ knot, the 10₁ knot, the 10₃₅ knot, the 10₅₈ knot, and the composite knot 5₂^* # 5₂,^[1] as well as the 9₁₆ knot, 10₇₆ knot, the 10₉₉ knot, the 10₁₂₂ knot, the 10₁₄₄ knot, the granny knot, and the composite knot 5₂ # 5₂.^[5] In addition, it is known that every twist knot with Arf invariant zero is a Lissajous knot.^[6]

Symmetry

Lissajous knots are highly symmetric, though the type of symmetry depends on whether or not the numbers 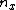, , and are all odd.

Odd case

If 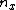, , and are all odd, then the point reflection across the origin 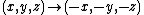is a symmetry of the Lissajous knot which preserves the knot orientation.

In general, a knot that has an orientation-preserving point reflection symmetry is known as strongly plus amphicheiral.^[7] This is a fairly rare property: only three prime knots with twelve or fewer crossings are strongly plus amphicheiral prime knot, the first of which has crossing number ten.^[8] Since this is so rare, ′most′ prime Lissajous knots lie in the even case.

Even case

If one of the frequencies (say 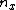) is even, then the 180° rotation around the x-axis is a symmetry of the Lissajous knot. In general, a knot that has a symmetry of this type is called 2-periodic, so every even Lissajous knot must be 2-periodic.

Consequences

The symmetry of a Lissajous knot puts severe constraints on the Alexander polynomial. In the odd case, the Alexander

polynomial of the Lissajous knot must be a perfect square.^[9] In the even case, the Alexander polynomial must be a perfect square modulo 2.^[10] In addition, the Arf invariant of a Lissajous knot must be zero. It follows that:

• The trefoil knot and figure-eight knot are not Lissajous.
• No torus knot can be Lissajous.
• No fibered 2-bridge knot can be Lissajous.

References

• Amelia Earhart (1976 TV Film)
• Amelia Earhart Birthplace
• Amelia Earhart Birthplace Museum
• Amelia Earhart Bridge
• Amelia Earhart Dam
• Amelia Earhart (disambiguation)
• Amelia Earhart Lives
• Amelia Earhart (Miniseries)
• Amelia Earhart (miniseries)
• Amelia Earhart Peak
• Amelia Earhart: The Final Flight
• Amelia Elizabeth Caroline
• Amelia Elizabeth Mary Rice
• Amelia Elizabeth Mary Rygate
• Amelia Fawcett
• Amelia Fiona J. Driver
• Amelia Fitzclarence
• Amelia Fournel
• Amelia Gray
• Amelia Green
• Amelia Greenhall
• Amelia Harris
• Amelia Hayes
• Amelia Hinten
• Amelia Hotham