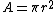“List of formulae involving π”的意思、由来-开放百科全书

词条

List of formulae involving π

释义

Euclidean geometry
Physics
Formulae yielding {{pi}}
Integrals Efficient infinite series Other infinite series Machin-like formulae Infinite series Infinite products Continued fractions Miscellaneous
See also
References
Further reading

{{DISPLAYTITLE:List of formulae involving {{pi}}}}{{Pi box}}

The following is a list of significant formulae involving the mathematical constant {{pi}}. The list contains only formulae whose significance is established either in the article on the formula itself, the article Pi, or the article Approximations of {{pi}}.

Euclidean geometry

where {{math|C}} is the circumference of a circle, {{math|d}} is the diameter.

where {{math|A}} is the area of a circle and {{math|r}} is the radius.

where {{math|V}} is the volume of a sphere and {{math|r}} is the radius.

where {{math|SA}} is the surface area of a sphere and {{math|r}} is the radius.

Physics

The cosmological constant:

Heisenberg's uncertainty principle:

Einstein's field equation of general relativity:

Coulomb's law for the electric force:

Magnetic permeability of free space:

Period of a simple pendulum with small amplitude:

Kepler's third law of planetary motion:

The buckling formula:

Formulae yielding {{pi}}

Integrals

(integral form of arctan over its entire domain, giving the period of tan).

(see Gaussian integral).

(when the path of integration winds once counterclockwise around 0. See also Cauchy's integral formula).

(see also Proof that 22/7 exceeds {{pi}}).

Efficient infinite series

(see also Double factorial)

(see Chudnovsky algorithm)

(see Srinivasa Ramanujan, Ramanujan–Sato series)

The following are efficient for calculating arbitrary binary digits of {{pi}}:

(see Bailey–Borwein–Plouffe formula)

Other infinite series

(see also Basel problem and Riemann zeta function)

, where B_2n is a Bernoulli number.

^[1]

(see Leibniz formula for pi)

(Euler, 1748)

After the first two terms, the signs are determined as follows: If the denominator is a prime of the form 4m − 1, the sign is positive; if the denominator is a prime of the form 4m + 1, the sign is negative; for composite numbers, the sign is equal the product of the signs of its factors.^[2]

Also:

where is the n-th Fibonacci number.

Some formulas relating {{pi}} and harmonic numbers are given here.

Machin-like formulae

(the original Machin's formula)

where is the n-th Fibonacci number.

Infinite series

Some infinite series involving pi are:^[3]

where is the Pochhammer symbol for the rising factorial. See also Ramanujan–Sato series.

Infinite products

(Euler)

where the numerators are the odd primes; each denominator is the multiple of four nearest to the numerator.

(see also Wallis product)

Viète's formula:

Continued fractions

For more on the third identity, see Euler's continued fraction formula.

(See also Continued fraction and Generalized continued fraction.)

Miscellaneous

(Stirling's approximation)

(Euler's identity)

(see Euler's totient function)

(see also Gamma function)

(where agm is the arithmetic–geometric mean)

(where is the remainder upon division of n by k)

(Riemann sum to evaluate the area of the unit circle)

(by Stirling's approximation)

References

1. ^Weisstein, Eric W. "Pi Formulas", MathWorld
2. ^Carl B. Boyer, A History of Mathematics, Chapter 21., pp. 488–489
3. ^{{cite web |title=The world of Pi |url=http://www.pi314.net/eng/ramanujan.php |author= Simon Plouffe / David Bailey |publisher=Pi314.net |date= |accessdate=2011-01-29}}
{{cite web|url=http://numbers.computation.free.fr/Constants/Pi/piSeries.html |title=Collection of series for {{pi}} |publisher=Numbers.computation.free.fr |date= |accessdate=2011-01-29}}