- Examples
- References
In mathematical logic, a literal is an atomic formula (atom) or its negation.
The definition mostly appears in proof theory (of classical logic), e.g. in conjunctive normal form and the method of resolution.
Literals can be divided into two types:
- A positive literal is just an atom.
- A negative literal is the negation of an atom.
For a literal 
, the complementary literal is a literal corresponding to the negation of ,
we can write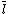 
to denote the complementary literal of . More precisely, if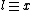 
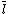then is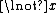 
and if 
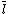then is 
.
In the context of a formula in the conjunctive normal form, a literal is pure if the literal's complement does not appear in the formula.
In Boolean functions, the variables that appear either in complemented or uncompleted form is a literal. For example, if 
, 
and 
are variables then the expressions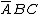 
contains three literal and 
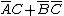contains three literals.[1]
Examples
In propositional calculus a literal is simply a propositional variable or its negation.
In predicate calculus a literal is an atomic formula or its negation, where an atomic formula is a predicate symbol applied to some terms,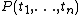 
with the terms recursively defined starting from constant symbols, variable symbols, and function symbols. For example, 
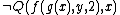is a negative literal with the constant symbol 2, the variable symbols x, y, the function symbols f, g, and the predicate symbol Q.
References
- {{cite book | author = Samuel R. Buss | chapter= An introduction to proof theory | editor = Samuel R. Buss | title=Handbook of proof theory | pages = 1–78 | url = http://math.ucsd.edu/~sbuss/ResearchWeb/handbookI/ | publisher = Elsevier | date = 1998 | isbn = 0-444-89840-9 }}
- Mertiňák
- Mert Kula
- Mert Matić
- Mert Muldur
- Mert Müldür
- Merton and Morden (disambiguation)
- Merton Borough Council
- Merton, Charles
- Merton council election, 2018
- Merton Davies
- Merton F. Utter
- Merton Hall, Norfolk
- Merton J. Batchelder
- Merton Laverne Lundquist
- Merton Laverne Lundquist Jr.
- Merton London Borough Council election, 1964
- Merton London Borough Council election, 1968
- Merton London Borough Council election, 1971
- Merton London Borough Council election, 1974
- Merton London Borough Council election, 1978
- Merton London Borough Council election, 1982
- Merton London Borough Council election, 1986
- Merton London Borough Council election, 1990
- Merton London Borough Council election, 1994
- Merton London Borough Council election, 1998