两个平面的关系liangge pingmian de guanxi
两个平面的相关位置有三种,即相交,重合,平行。两个平面arx+bry+crz+dr = 0 (ar2+br2+cr2≠ 0,r=1,2)相交的充要条件是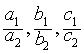 相交的充要条件是 三者不全相等;重合的充要条件是
相交的充要条件是 三者不全相等;重合的充要条件是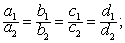 充要条件是;平行的充要条件是a1/a2
充要条件是;平行的充要条件是a1/a2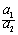
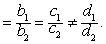 如果平面的方程是向量形式,则两个平面mr ·P+dr=0 (r=1,2)相交的充要条件是m1×m2≠0;重合的充要条件是m1 × m2=0,d1m2-d2m1=0;平行的充要条件是m1×m2=0,d1m2-d2m1≠0。且当两个平面相交时,m1×m2将是交线上的一个向量。
如果平面的方程是向量形式,则两个平面mr ·P+dr=0 (r=1,2)相交的充要条件是m1×m2≠0;重合的充要条件是m1 × m2=0,d1m2-d2m1=0;平行的充要条件是m1×m2=0,d1m2-d2m1≠0。且当两个平面相交时,m1×m2将是交线上的一个向量。
如果以代数的角度考虑,则两个平面arx+bry+crz+dr=0 (ar2+br2+cr2≠0,r=1,2)相交的充要条件是RC=RA=2;重合的充要条件是RC=RA=1;平行的充要条件是RC=1,RA=2。这里RC和RA分别是上面两个方程的系数矩阵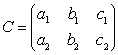 和增广矩阵A=
和增广矩阵A=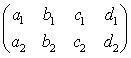 的秩。
的秩。
两个平面相交时,产生四个二面角,形成两对对棱二面角并且每对也都相等。二平面相交所构成的两个相邻二面角中有一个等于它们的两个法线向量的交角. 设两个平面Nr0 ·P-pr=0 (r=1,2)相交,则它们交角的余弦等于± (N10 ·N20)。两个平面Nr0 ·P-pr=0 (r=1,2)垂直的充要条件是N10 ·N20=0。两个平面arx+bry+crz+dr=0 (ar2+br2+cr2≠0,r=1,2)如果相交,则它们交角的余弦等于
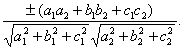
设两个平面Nr0 ·P-pr=0 (r=1,2)相交,则它们的两个平分角面的方程是(N10=N20)。P-(p1-p2)=0和 (N10+N20) ·P-(p1+p2) =0,且二平分角面是互相垂直的。写成坐标形式就是,两个平面arx+bry+crz+dr=0 (ar2+br2+cr2≠0,r=1,2) 的两个平分角面方程是
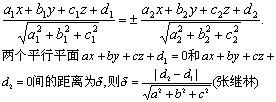
两个平行平面ax+by+cz+d1=0和az+by+cz+d2=0间的距离为d,则