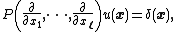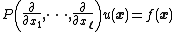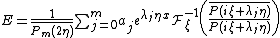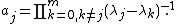“Malgrange–Ehrenpreis theorem”的意思、由来-开放百科全书

词条

Malgrange–Ehrenpreis theorem

释义

Proofs
References

In mathematics, the Malgrange–Ehrenpreis theorem states that every non-zero linear differential operator with constant coefficients has a Green's function. It was first proved independently by {{harvs|txt=yes|first=Leon |last=Ehrenpreis|authorlink=Leon Ehrenpreis|year1=1954|year2=1955}} and

{{Harvs|txt=yes|first=Bernard|last=Malgrange|authorlink=Bernard Malgrange|year=1955–1956}}.

This means that the differential equation

where P is a polynomial in several variables and δ is the Dirac delta function, has a distributional solution u. It can be used to show that

has a solution for any compactly supported distribution f. The solution is not unique in general.

The analogue for differential operators whose coefficients are polynomials (rather than constants) is false: see Lewy's example.

Proofs

The original proofs of Malgrange and Ehrenpreis were non-constructive as they used the Hahn–Banach theorem. Since then several constructive proofs have been found.

There is a very short proof using the Fourier transform and the Bernstein–Sato polynomial, as follows. By taking Fourier transforms the Malgrange–Ehrenpreis theorem is equivalent to the fact that every non-zero polynomial P has a distributional inverse. By replacing P by the product with its complex conjugate, one can also assume that P is non-negative. For non-negative polynomials P the existence of a distributional inverse follows from the existence of the Bernstein–Sato polynomial, which implies that P^s can be analytically continued as a meromorphic distribution-valued function of the complex variable s; the constant term of the Laurent expansion of P^s at s = −1 is then a distributional inverse of P.

Other proofs, often giving better bounds on the growth of a solution, are given in {{harv|Hörmander|1983a|loc=Theorem 7.3.10}}, {{harv|Reed|Simon|1975|loc=Theorem IX.23, p. 48}} and {{harv|Rosay|1991}}.

{{harv|Hörmander|1983b|loc=chapter 10}} gives a detailed discussion of the regularity properties of the fundamental solutions.

A short constructive proof was presented in {{harv|Wagner|2009|loc=Proposition 1, p. 458}}:

is a fundamental solution of P(∂), i.e., P(∂)E = δ, if P_m is the principal part of P, η ∈ Rⁿ with P_m(η) ≠ 0, the real numbers λ₀, ..., λ_m are pairwise different, and

References

{{citation|last=Ehrenpreis|first= Leon |title=Solution of some problems of division. I. Division by a polynomial of derivation. |journal=Amer. J. Math.|volume= 76|year=1954|pages= 883–903|issue=4|doi=10.2307/2372662|jstor=2372662|mr=0068123}}
{{citation |last=Ehrenpreis|first= Leon |title=Solution of some problems of division. II. Division by a punctual distribution |journal=Amer. J. Math.|volume= 77|year=1955|pages= 286–292 |issue=2|doi=10.2307/2372532|jstor=2372532 |mr=0070048}}
{{citation|first=L.|last= Hörmander|title=The analysis of linear partial differential operators I|series= Grundl. Math. Wissenschaft. |volume= 256 |publisher= Springer |year=1983a|isbn=978-3-540-12104-6|mr=0717035 |doi=10.1007/978-3-642-96750-4}}
{{citation| first=L.|last= Hörmander|title=The analysis of linear partial differential operators II|series= Grundl. Math. Wissenschaft. |volume= 257 |publisher= Springer |year=1983b|isbn=978-3-540-12139-8| mr=0705278 |doi=10.1007/978-3-642-96750-4}}
{{citation |last=Malgrange|first= Bernard |title=Existence et approximation des solutions des équations aux dérivées partielles et des équations de convolution

|journal=Annales de l'Institut Fourier |volume= 6 |year=1955–1956|pages= 271–355 |url=http://aif.cedram.org/aif-bin/item?id=AIF_1956__6__271_0 |mr=0086990 |doi=10.5802/aif.65}}

{{citation |last=Reed|first= Michael|last2= Simon|first2= Barry|author2-link=Barry Simon |title=Methods of modern mathematical physics. II. Fourier analysis, self-adjointness |publisher=Academic Press Harcourt Brace Jovanovich, Publishers|location=New York-London|year= 1975|pages= xv+361|isbn =978-0-12-585002-5|mr=0493420}}
{{citation |last=Rosay|first= Jean-Pierre |title=A very elementary proof of the Malgrange-Ehrenpreis theorem |journal=Amer. Math. Monthly|volume= 98 |year=1991|issue= 6|pages= 518–523|doi =10.2307/2324871|mr=1109574|jstor=2324871}}
{{springer|id=M/m120090|title=Malgrange–Ehrenpreis theorem|first=Jean-Pierre |last=Rosay}}
{{citation|last=Wagner|first=Peter |title=A new constructive proof of the Malgrange-Ehrenpreis theorem |journal=Amer. Math. Monthly|volume=116|year=2009|issue= 5|pages= 457–462|doi=10.4169/193009709X470362|mr=2510844|citeseerx=10.1.1.488.6651 }}

2 : Differential equations|Theorems in analysis

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。