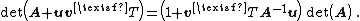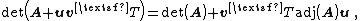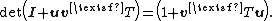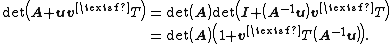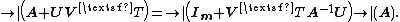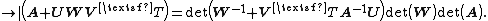1. Statement

2. Proof

3. Application

4. Generalization

5. See also

6. References

In mathematics, in particular linear algebra, the matrix determinant lemma computes the determinant of the sum of an invertible matrix A and the dyadic product, u{{thinsp}}v^T, of a column vector u and a row vector v^T.^[1][2]

Statement

Suppose A is an invertible square matrix and u, v are column vectors. Then the matrix determinant lemma states that

Here, uv^T is the outer product of two vectors u and v.

The theorem can also be stated in terms of the adjugate matrix of A:

in which case it applies whether or not the square matrix A is invertible.

Proof

First the proof of the special case A = I follows from the equality:^[3]

The determinant of the left hand side is the product of the determinants of the three matrices. Since the first and third matrix are triangular matrices with unit diagonal, their determinants are just 1. The determinant of the middle matrix is our desired value. The determinant of the right hand side is simply (1 + v^Tu). So we have the result:

Then the general case can be found as:

Application

If the determinant and inverse of A are already known, the formula provides a numerically cheap way to compute the determinant of A corrected by the matrix uv^T. The computation is relatively cheap because the determinant of A + uv^T does not have to be computed from scratch (which in general is expensive). Using unit vectors for u and/or v, individual columns, rows or elements^[4] of A may be manipulated and a correspondingly updated determinant computed relatively cheaply in this way.

When the matrix determinant lemma is used in conjunction with the Sherman–Morrison formula, both the inverse and determinant may be conveniently updated together.

Generalization

Suppose A is an invertible n-by-n matrix and U, V are n-by-m matrices. Then

In the special case 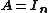this is Sylvester's theorem for determinants.

Given additionally an invertible m-by-m matrix W, the relationship can also be expressed as

See also

• The Sherman–Morrison formula, which shows how to update the inverse, A⁻¹, to obtain (A + uv^T)⁻¹.
• The Woodbury formula, which shows how to update the inverse, A⁻¹, to obtain (A + UCV^T)⁻¹.
• The binomial inverse theorem for (A + UCV^T)⁻¹.

References

• LG Optimus Black
• Lg optimus c
• LG Optimus Chat
• LG Optimus Chic
• LG Optimus Chic E720
• LG Optimus G
• LG Optimus G2
• LG Optimus G Pro
• LG Optimus L2
• LG Optimus L3
• LG Optimus L4 II
• LG Optimus L5
• LG Optimus L5 II
• LG Optimus L7
• LG Optimus L70
• LG Optimus L9
• LG Optimus LTE
• Lg optimus m
• LG Optimus One P500
• LG Optimus Pad
• LG Optimus Pad LTE
• Lg optimus s
• LG Optimus S
• LG Optimus Series
• LG Optimus Slider