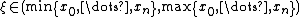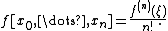“Mean value theorem (divided differences)”的意思、由来-开放百科全书

词条

Mean value theorem (divided differences)

释义

Statement of the theorem
Proof
Applications
References

In mathematical analysis, the mean value theorem for divided differences generalizes the mean value theorem to higher derivatives.^[1]

Statement of the theorem

For any n + 1 pairwise distinct points x₀, ..., x_n in the domain of an n-times differentiable function f there exists an interior point

where the nth derivative of f equals n ! times the nth divided difference at these points:

For n = 1, that is two function points, one obtains the simple mean value theorem.

Proof

Let be the Lagrange interpolation polynomial for f at x₀, ..., x_n.

Then it follows from the Newton form of that the highest term of is .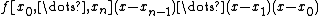

Let be the remainder of the interpolation, defined by 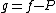. Then has zeros: x₀, ..., x_n.

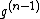By applying Rolle's theorem first to , then to , and so on until , we find that has a zero . This means that

,

Applications

The theorem can be used to generalise the Stolarsky mean to more than two variables.

References

1. ^{{cite journal|last=de Boor|first=C.|title=Divided differences|journal=Surv. Approx. Theory|year=2005|volume=1|pages=46–69|authorlink=Carl R. de Boor|mr=2221566}}

1 : Finite differences

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。