湾流wanliu
北大西洋副热带总环流系统中的西部边界流。它是由北赤道流和南赤道流越过赤道的北分支汇合而成的世界大洋中最强的暖流。以往“湾流”这一名称是指从墨西哥湾发源的洋流。现在对“湾流”广义的说法,是指从墨西哥湾开始,沿北美洲东岸北上,然后向东横贯大西洋,至欧洲西北沿岸,最后穿过挪威海进入北冰洋的整个系统。在海洋学上,湾流系统被分为三个组成部分:佛罗里达海流、湾流和北大西洋海流。其中湾流为这个系统的主体段,它从美国东岸哈特勒斯角附近(35°附近),海流离开海岸向东进入4000~5000米的深水区,至格兰德滩(Grand Banks)以南,约西经45°附近,海流都保持在狭窄带内,流势也最强。湾流的表面宽度介于100~150公里之间,是斜压性很强的地转流,其面向流向的左侧是高密度的低温沿岸水,右侧是密度稍低而温暖的马尾藻海水。表面最大流速可达250厘米/秒,流量可高达150×106米3/秒,相当于全世界河流流量总和的120倍。湾流表层海水的温度和盐度年平均值分别介于25~26℃和36.2~36.4‰之间。湾流所到之处影响深度一般约700~800米,但湾流离开哈特勒斯角之后,流的厚度可超过4000米。
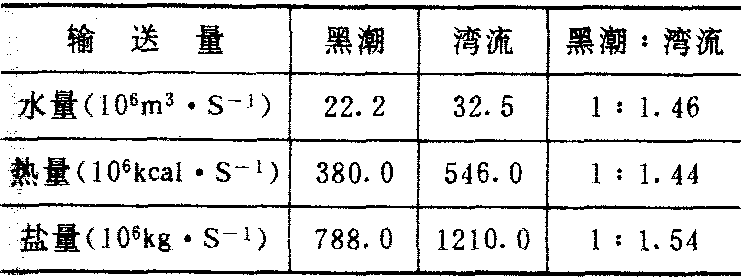
湾流是一支巨大的暖流,它与黑潮相比,无论在水量、热量和盐量输送等方面都大于黑潮(见表)。大量暖水北运,对北部沿岸气候发生巨大影响,例如处于北纬55~70°的加拿大东岸,年平均气温为-10~0℃,而欧洲的西部海岸,年平均气温则高达0~10℃。另外,温暖的海水,蒸发较强,降水量也较同纬度大洋西部要丰沛得多。温和而又湿润的气候,使常绿的针叶林最北界可达北纬70°左右。极圈之内的巴伦支海,虽然湾流到此已为强弩之末,但南部海域冬季也不封冻。苏联的摩尔曼斯克位于北纬69°,也是一个不冻港。
北纬27°~37°湾流和黑潮的水量、热量、盐量的输送比较
湾流
即“墨西哥湾暖流”。
湾流
又称墨西哥湾流。广义的湾流是指从佛罗里达海峡流向欧洲西北部海域的暖流系统。狭义的湾流仅限于从美国东岸哈特勒斯角至纽芬兰东南沿岸的一段大西洋西部边界洋流,是按顺时针方向流动的北大西洋环流的一个组成部分。湾流从153 km宽的佛罗里达海峡流出,时速为6.5km,水量达26×106 m3/s,相当于密西西比河的1000倍。在巴哈马群岛以北与安德罗斯暖流汇合,转向东北,此段称为佛罗里达海流,它是湾流的源头。继之,这股强大的海流沿美国东海岸一直流至哈特勒斯角,构成湾流的主体。再经纽芬兰海岸向东,汇入大西洋漂流。冬季时,新英格兰沿岸湾流的表层水温比距离241 km的西北海域水温高11℃。挪威西岸的气温比同纬度的气温要高出22℃。挪威的卑尔根位于60°N,最冷月平均气温为1℃,而加拿大新斯科舍省的哈利法克斯,其位置虽比卑尔根偏南1609 km,而最冷月平均气温却为-5℃。英格兰西南部的德文郡南部居然能栽培亚热带的柠檬树。