- References
In knot theory, the Milnor conjecture says that the slice genus of the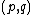 
torus knot is
It is in a similar vein to the Thom conjecture.
It was first proved by gauge theoretic methods by Peter Kronheimer and Tomasz Mrowka.[1] Jacob Rasmussen later gave a purely combinatorial proof using Khovanov homology, by means of the s-invariant.[2]
References
1. ^{{citation|title=Gauge theory for embedded surfaces, I|first1=P. B.|last1=Kronheimer|authorlink1=Peter Kronheimer|first2=T. S.|last2=Mrowka|journal=Topology|volume=32|issue=4|year=1993|pages=773–826|doi=10.1016/0040-9383(93)90051-V}}.
2. ^{{cite arxiv|eprint=math.GT/0402131 |title=Khovanov homology and the slice genus|first=Jacob A.|last=Rasmussen|year=2004}}.
{{knottheory-stub}}2. ^{{cite arxiv|eprint=math.GT/0402131 |title=Khovanov homology and the slice genus|first=Jacob A.|last=Rasmussen|year=2004}}.
4 : Geometric topology|Knot theory|4-manifolds|Conjectures that have been proved
- Phytolacca japonica
- Phytoliriomyza
- Phytoliriomyza clara
- Phytoliriomyza dorsata
- Phytoliriomyza felti
- Phytoliriomyza melampyga
- Phytologist
- Phytologist (journal)
- Phytomedicine
- Phytomedicine (Journal)
- Phytomelan
- Phytomelanin
- Phytomelanous
- Phytometra apicata
- Phytometra obliqualis
- Phytometra orgiae
- Phytomimia
- Phytomimia chlorophylla
- Phytomimia cynegetis
- Phytomimia pyrrhophthalma
- Phytomimia redundans
- Phytomimia silvicolor
- Phytomonas
- Phytomy
- Phytomyptera flavipes