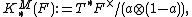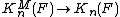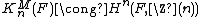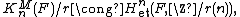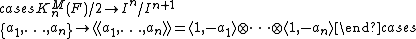“Milnor K-theory”的意思、由来-开放百科全书

词条

Milnor K-theory

释义

Definition
Examples
Applications
References

In mathematics, Milnor K-theory is an invariant of fields defined by {{harvs|txt|last=Milnor|first=John|year=1970|authorlink=John Milnor}}. Originally viewed as an approximation to algebraic K-theory, Milnor K-theory has turned out to be an important invariant in its own right.

Definition

The calculation of K₂ of a field by Hideya Matsumoto led Milnor to the following, seemingly naive, definition of the "higher" K-groups of a field F:

the quotient of the tensor algebra over the integers of the multiplicative group 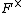by the two-sided ideal generated by:

The nth Milnor K-group 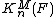is the nth graded piece of this graded ring; for example, 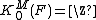and 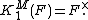There is a natural homomorphism

from the Milnor K-groups of a field to the Quillen K-groups, which is an isomorphism for n ≤ 2 but not for larger n, in general. For nonzero elements a₁, ..., a_n in F, the symbol {a₁, ..., a_n} in 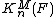means the image of a₁ ⊗ ... ⊗ a_n in the tensor algebra. Every element of Milnor K-theory can be written as a finite sum of symbols. The fact that {a, 1−a} = 0 in 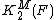for a in F − {0,1} is sometimes called the Steinberg relation.

The ring 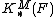is graded-commutative.^[1]

Examples

We have for n ≥ 2, while 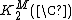is an uncountable uniquely divisible group.^[2] Also, 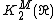is the direct sum of a cyclic group of order 2 and an uncountable uniquely divisible group; 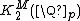is the direct sum of the multiplicative group of 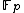and an uncountable uniquely divisible group; 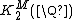is the direct sum of the cyclic group of order 2 and cyclic groups of order for all odd prime .

Applications

Milnor K-theory plays a fundamental role in higher class field theory, replacing 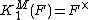in the one-dimensional class field theory.

Milnor K-theory fits into the broader context of motivic cohomology, via the isomorphism

of the Milnor K-theory of a field with a certain motivic cohomology group.^[3] In this sense, the apparently ad hoc definition of Milnor K-theory becomes a theorem: certain motivic cohomology groups of a field can be explicitly computed by generators and relations.

A much deeper result, the Bloch-Kato conjecture (also called the norm residue isomorphism theorem), relates Milnor K-theory to Galois cohomology or etale cohomology:

for any positive integer r invertible in the field F. This was proved by Voevodsky, with contributions by Rost and others.^[4] This includes the Merkurjev−Suslin theorem and the Milnor conjecture as special cases (the cases n = 2 and r = 2, respectively).

Finally, there is a relation between Milnor K-theory and quadratic forms. For a field F of characteristic not 2, define the fundamental ideal I in the Witt ring of quadratic forms over F to be the kernel of the homomorphism 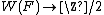given by the dimension of a quadratic form, modulo 2. Milnor defined a homomorphism:

where 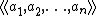denotes the class of the n-fold Pfister form.^[5]

Orlov, Vishik, and Voevodsky proved another statement called the Milnor conjecture, namely that this homomorphism 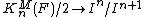is an isomorphism.^[6]

References

1. ^Gille & Szamuely (2006), p. 184.
2. ^An abelian group is uniquely divisible if it is a vector space over the rational numbers.
3. ^Mazza, Voevodsky, Weibel (2005), Theorem 5.1.
4. ^Voevodsky (2011).
5. ^Elman, Karpenko, Merkurjev (2008), sections 5 and 9.B.
6. ^Orlov, Vishik, Voevodsky (2007).

{{Citation | title=Algebraic and geometric theory of quadratic forms | author1-first=Richard | author1-last=Elman | author1-link=Richard Elman (mathematician) | author2-first=Nikita | author2-last=Karpenko | author3-first=Alexander | author3-last=Merkurjev | author3-link=Alexander Merkurjev | publisher=American Mathematical Society | year=2008 | isbn=978-0-8218-4329-1 | mr=2427530}}
{{cite book | last1=Gille | first1=Philippe | last2=Szamuely | first2=Tamás | title=Central simple algebras and Galois cohomology | series=Cambridge Studies in Advanced Mathematics | volume=101 | location=Cambridge | publisher=Cambridge University Press | year=2006 | isbn=0-521-86103-9 | zbl=1137.12001 | mr=2266528}}
{{Citation | author1-first=Carlo | author1-last=Mazza | author2-first=Vladimir | author2-last=Voevodsky | author2-link=Vladimir Voevodsky | author3-first=Charles | author3-last=Weibel | author3-link=Charles Weibel | title= Lectures in Motivic Cohomology | url= http://math.rutgers.edu/~weibel/motiviclectures.html | series=Clay Mathematical Monographs, vol. 2| publisher= American Mathematical Society| isbn=978-0-8218-3847-1 | year=2006 | mr=2242284}}
{{Citation | last1=Milnor | first1=John Willard | author1-link= John Milnor | title=Algebraic K-theory and quadratic forms | others=With an appendix by J. Tate | mr=0260844 | zbl=0199.55501 | year=1970 | journal=Inventiones Mathematicae | issn=0020-9910 | volume=9 | pages=318–344 | doi=10.1007/BF01425486| bibcode=1970InMat...9..318M }}
{{Citation | title=An exact sequence for K^M/2 with applications to quadratic forms | author1-first=Dmitri | author1-last=Orlov | author2-first=Alexander | author2-last=Vishik | author3-first=Vladimir | author3-last=Voevodsky | author3-link=Vladimir Voevodsky | journal=Annals of Mathematics | volume=165 | year=2007 | pages=1–13 | doi=10.4007/annals.2007.165.1 | mr=2276765| arxiv=math/0101023 }}
{{Citation | author1-last=Voevodsky|author1-first=Vladimir|author1-link=Vladimir Voevodsky | title=On motivic cohomology with Z/l-coefficients|journal=Annals of Mathematics|date=2011|volume=174|issue=1|pages=401–438|doi=10.4007/annals.2011.174.1.11|url=http://annals.math.princeton.edu/2011/174-1/p11 | mr=2811603|arxiv=0805.4430}}

1 : K-theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。