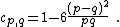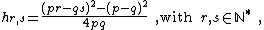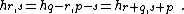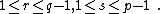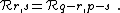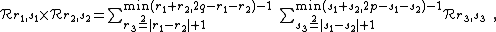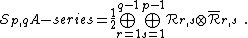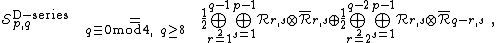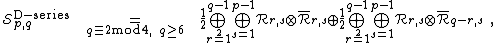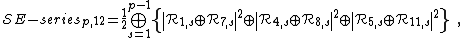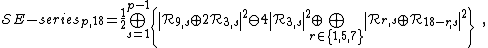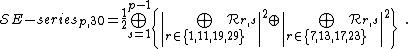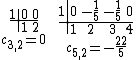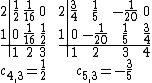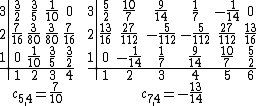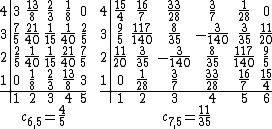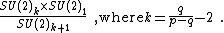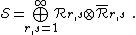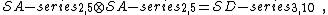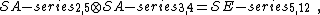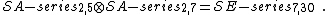- Relevant representations of the Virasoro algebra Representations Fusion rules
- Classification A-series minimal models: the diagonal case D-series minimal models E-series minimal models
- Examples
- Related conformal field theories Coset realizations Generalized minimal models Liouville theory Products of minimal models
- References
In theoretical physics, a minimal model or Virasoro minimal model is a two-dimensional conformal field theory whose spectrum is built from finitely many irreducible representations of the Virasoro algebra.
Minimal models have been classified and solved, and found to obey an ADE classification. [1]
The term minimal model can also refer to a rational CFT based on an algebra that is larger than the Virasoro algebra, such as a W-algebra.
Relevant representations of the Virasoro algebra
Representations
In minimal models, the central charge of the Virasoro algebra takes values of the type
where 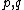 are coprime integers such that
are coprime integers such that 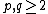 .
.
Then the conformal dimensions of degenerate representations are
and they obey the identities
The spectrums of minimal models are made of irreducible, degenerate lowest-weight representations of the Virasoro algebra, whose conformal dimensions are of the type 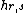 with
with
Such a representation 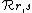 is a coset of a Verma module by its infinitely many nontrivial submodules. It is unitary if and only if
is a coset of a Verma module by its infinitely many nontrivial submodules. It is unitary if and only if 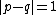 . At a given central charge, there are
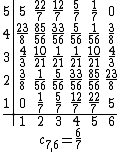
. At a given central charge, there are 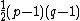 distinct representations of this type. The set of these representations, or of their conformal dimensions, is called the Kac table with parameters
distinct representations of this type. The set of these representations, or of their conformal dimensions, is called the Kac table with parameters 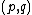 . The Kac table is usually drawn as a rectangle of size
. The Kac table is usually drawn as a rectangle of size  , where each representation appears twice
, where each representation appears twice
due to the relation
Fusion rules
The fusion rules of the multiply degenerate representations 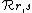 encode constraints from all their null vectors. They can therefore be deduced from the fusion rules of simply degenerate representations, which encode constraints from individual null vectors.[2] Explicitly, the fusion rules are
encode constraints from all their null vectors. They can therefore be deduced from the fusion rules of simply degenerate representations, which encode constraints from individual null vectors.[2] Explicitly, the fusion rules are
where the sums run by increments of two.
Classification
A-series minimal models: the diagonal case
For any coprime integers  such that
such that 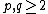 , there exists a diagonal minimal model whose spectrum contains one copy of each distinct representation in the Kac table:
, there exists a diagonal minimal model whose spectrum contains one copy of each distinct representation in the Kac table:
The  and
and  models are the same.
models are the same.
The OPE of two fields involves all the fields that are allowed by the fusion rules of the corresponding representations.
D-series minimal models
A D-series minimal model with the central charge 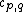 exists if
exists if  or
or  is even and at least
is even and at least 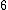 . Using the symmetry
. Using the symmetry 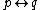
we assume that  is even, then
is even, then  is odd. The spectrum is
is odd. The spectrum is
where the sums over  run by increments of two.
run by increments of two.
In any given spectrum, each representation has multiplicity one, except the representations of the type 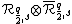 if
if 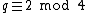 , which have multiplicity two. These representations indeed appear in both terms in our formula for the spectrum.
, which have multiplicity two. These representations indeed appear in both terms in our formula for the spectrum.
The OPE of two fields involves all the fields that are allowed by the fusion rules of the corresponding representations, and that respect the conservation of diagonality: the OPE of one diagonal and one non-diagonal field yields only non-diagonal fields, and the OPE of two fields of the same type yields only diagonal fields.
[2]For this rule, one copy of the representation 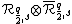
counts as diagonal, and the other copy as non-diagonal.
E-series minimal models
There are three series of E-series minimal models. Each series exists for a given value of 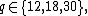 for any
for any 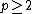 that is coprime with
that is coprime with  . (This actually implies
. (This actually implies 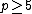 .) Using the notation
.) Using the notation 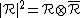 , the spectrums read:
, the spectrums read:
Examples
The following A-series minimal models are related to well-known physical systems:[3]
-
 : trivial CFT,
: trivial CFT, -
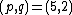 : Yang-Lee edge singularity,
: Yang-Lee edge singularity, -
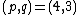 : Ising model at criticality,
: Ising model at criticality, -
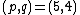 : tricritical Ising model.
: tricritical Ising model.
The following D-series minimal models are related to well-known physical systems:
-
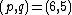 : 3-state Potts model,
: 3-state Potts model, -
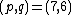 : tricritical 3-state Potts model.
: tricritical 3-state Potts model.
The Kac tables of these models, together with a few other Kac tables with 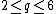 , are:
, are:
Related conformal field theories
Coset realizations
The A-series minimal model with indices  coincides with the following coset of WZW models:[3]
coincides with the following coset of WZW models:[3]
Assuming 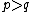 , the level
, the level  is integer if and only if
is integer if and only if 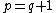 i.e. if and only if the minimal model is unitary.
i.e. if and only if the minimal model is unitary.
There exist other realizations of certain minimal models, diagonal or not, as cosets of WZW models, not necessarily based on the group 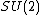 .[3]
.[3]
Generalized minimal models
For any central charge 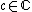 , there is a diagonal CFT whose spectrum is made of all degenerate representations,
, there is a diagonal CFT whose spectrum is made of all degenerate representations,
When the central charge tends to 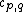 , the generalized minimal models tend to the corresponding A-series minimal model.[4] This means in particular that the degenerate representations that are not in the Kac table decouple.
, the generalized minimal models tend to the corresponding A-series minimal model.[4] This means in particular that the degenerate representations that are not in the Kac table decouple.
Liouville theory
Since Liouville theory reduces to a generalized minimal model when the fields are taken to be degenerate,[4] it further reduces to an A-series minimal model when the central charge is then sent to 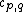 .
.
Moreover, A-series minimal models have a well-defined limit as 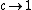 : a diagonal CFT with a continuous spectrum called Runkel-Watts theory,[5] which coincides with the limit of Liouville theory when
: a diagonal CFT with a continuous spectrum called Runkel-Watts theory,[5] which coincides with the limit of Liouville theory when 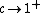 .[6]
.[6]
Products of minimal models
There are three cases of minimal models that are products of two minimal models.[7]
At the level of their spectrums, the relations are:
References
2. ^ I. Runkel, "Structure constants for the D series Virasoro minimal models", [https://arxiv.org/abs/hep-th/9908046 hep-th/9908046]
3. ^1 2 3 P. Di Francesco, P. Mathieu, and D. Sénéchal, Conformal Field Theory, 1997, {{ISBN|0-387-94785-X}}
4. ^1 S. Ribault, "Conformal field theory on the plane", [https://arxiv.org/abs/1406.4290 arXiv:1406.4290]
5. ^I. Runkel, G. Watts, "A Nonrational CFT with c = 1 as a limit of minimal models", [https://arxiv.org/abs/hep-th/0107118 arXiv:hep-th/0107118]
6. ^V. Schomerus, "Rolling tachyons from Liouville theory",[https://arxiv.org/abs/hep-th/0306026 arXiv:hep-th/0306026]
7. ^T. Quella, I. Runkel, G. Watts, "Reflection and Transmission for Conformal Defects", [https://arxiv.org/abs/hep-th/0611296 arxiv:hep-th/0611296]
- Rick Middleton (football player)
- Rick Mills
- Rick 'Minty' Peterson
- Rick Mitchell (athlete)
- Rick Mitchell (meteorologist)
- Rick Moffat
- Rick Mofina
- Rick Moody (coach)
- Rick Moranis in Gravedale High
- Rick Moses
- Rick Mueller
- Rick Neelan
- Rick Neilsen
- Rick Nevin
- Rick Newell
- Rick Newsom
- Rick Noji
- Rick Norton
- Rick Nowlin
- Rick Nugent
- Rick Nuzum
- Rick O'Connell
- Rick Olseen
- Rick Orman
- Rick Ownbey