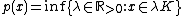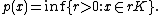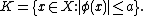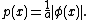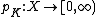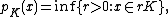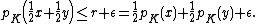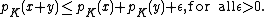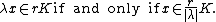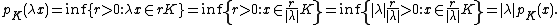“Minkowski functional”的意思、由来-开放百科全书

词条

Minkowski functional

释义

Examples
Example 1 Example 2
Definition
Convexity of K Balancedness of K
See also
Notes
References

In mathematics, in the field of functional analysis, a Minkowski functional is a function that recovers a notion of distance on a linear space.

Let K be a symmetric (i.e. if it contains x it also contains -x) convex body in a linear space V. We define a function p on V as

This is the Minkowski functional of K.^[1] Usually it is assumed that K is such that the set of is never empty, but sometimes the set is allowed to be empty and then p(x) is defined as infinity.

Examples

Example 1

Consider a normed vector space , with the norm ||·||. Let be the unit ball in . Define a function 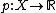by

One can see that 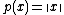, i.e. is just the norm on . The function p is a special case of a Minkowski functional.

Example 2

Let X be a vector space without topology with underlying scalar field . Take 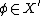, the algebraic dual of , i.e. 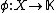is a linear functional on . Fix . Let the set be given by

Again we define

Then

The function p(x) is another instance of a Minkowski functional. It has the following properties:

It is subadditive: ,
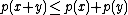It is homogeneous: for all ,
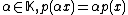It is nonnegative.

Therefore, is a seminorm on , with an induced topology. This is characteristic of Minkowski functionals defined via "nice" sets. There is a one-to-one correspondence between seminorms and the Minkowski functional given by such sets. What is meant precisely by "nice" is discussed in the section below.

Notice that, in contrast to a stronger requirement for a norm, need not imply . In the above example, one can take a nonzero from the kernel of . Consequently, the resulting topology need not be Hausdorff.

Definition

The above examples suggest that, given a (complex or real) vector space X and a subset K, one can define a corresponding Minkowski functional

which is often called the gauge of .

It is implicitly assumed in this definition that 0 ∈ K and the set {r > 0: x ∈ r K} is nonempty for every x. In order for p_K to have the properties of a seminorm, additional restrictions must be imposed on K. These conditions are listed below.

The set K being convex implies the subadditivity of p_K.
Homogeneity, i.e. p_K(α x) = |α| p_K(x) for all α, is ensured if K is balanced, meaning α K ⊂ K for all |α| ≤ 1.

A set K with these properties is said to be absolutely convex.

Convexity of K

A simple geometric argument that shows convexity of K implies subadditivity is as follows. Suppose for the moment that p_K(x) = p_K(y) = r. Then for all ε > 0, we have x, y ∈ (r + ε) K = K' . The assumption that K is convex means K' is also. Therefore, ½ x + ½ y is in K' . By definition of the Minkowski functional p_K, one has

But the left hand side is ½ p_K(x + y), i.e. the above becomes

This is the desired inequality. The general case p_K(x) > p_K(y) is obtained after the obvious modification.

Note Convexity of K, together with the initial assumption that the set {r > 0: x ∈ r K} is nonempty, implies that K is absorbing.

Balancedness of K

Notice that K being balanced implies that

Therefore

Notes

1. ^Thompson (1996) p.17

References

{{cite book | title=Minkowski Geometry | series=Encyclopedia of Mathematics and Its Applications | first=Anthony C. | last=Thompson | publisher=Cambridge University Press | year=1996 | isbn=0-521-40472-X }}

3 : Functional analysis|Convex analysis|Hermann Minkowski

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。