- Definition of a monotone class
- Monotone class theorem for sets Statement
- Monotone class theorem for functions Statement Proof
- Results and applications
- References
In measure theory and probability, the monotone class theorem connects monotone classes and sigma-algebras. The theorem says that the smallest monotone class containing an algebra of sets G is precisely the smallest σ-algebra containing G. It is used as a type of transfinite induction to prove many other theorems, such as Fubini's theorem.
Definition of a monotone class
A monotone class is a class M of sets that is closed under countable monotone unions and intersections, i.e. if 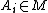 and
and 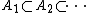 then
then  , and similarly in the other direction.
, and similarly in the other direction.
Monotone class theorem for sets
Statement
Let G be an algebra of sets and define M(G) to be the smallest monotone class containing G. Then M(G) is precisely the σ-algebra generated by G, i.e. σ(G) = M(G).
Monotone class theorem for functions
Statement
Let  be a {{pi}}-system that contains
be a {{pi}}-system that contains  and let
and let  be a collection of functions from
be a collection of functions from  to R with the following properties:
to R with the following properties:
(1) If  , then
, then 
(2) If 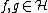 , then
, then  and
and 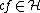 for any real number
for any real number 
(3) If 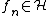 is a sequence of non-negative functions that increase to a bounded function
is a sequence of non-negative functions that increase to a bounded function  , then
, then 
Then  contains all bounded functions that are measurable with respect to
contains all bounded functions that are measurable with respect to 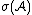 , the sigma-algebra generated by
, the sigma-algebra generated by 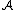
Proof
The following argument originates in Rick Durrett's Probability: Theory and Examples.
[1]The assumption 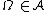 , (2) and (3) imply that
, (2) and (3) imply that 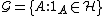 is a λ-system. By (1) and the {{pi}}−λ theorem,
is a λ-system. By (1) and the {{pi}}−λ theorem,  . (2) implies
. (2) implies  contains all simple functions, and then (3) implies that
contains all simple functions, and then (3) implies that  contains all bounded functions measurable with respect to
contains all bounded functions measurable with respect to 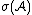 .
.
Results and applications
As a corollary, if G is a ring of sets, then the smallest monotone class containing it coincides with the sigma-ring of G.
By invoking this theorem, one can use monotone classes to help verify that a certain collection of subsets is a sigma-algebra.
The monotone class theorem for functions can be a powerful tool that allows statements about particularly simple classes of functions to be generalized to arbitrary bounded and measurable functions.
References
- Richard Morgan (author)
- Richard Morgan (Chief Justice)
- Richard Morgan (cricketer)
- Richard Morgan (English judge)
- Richard Morgan (lawyer)
- Richard Morgan (MP for Gloucester)
- Richard Morris (archaeologist)
- Richard Morris (footballer)
- Richard Morris Hunt Memorial
- Richard Morris (New York)
- Richard Morris (New York judge)
- Richard morrison film titles
- Richard Morrison (Film titles designer)
- Richard Morrison (film titles designer)
- Richard Morrison (music critic)
- Richard Morrissey
- Richard Morris (UK politician)
- Richard Morris (US politician)
- Richard Morse
- Richard Morse (disambiguation)
- Richard Morthland
- Richard Morton
- Richard Morton (disambiguation)
- Richard Morysine
- Richard Moryson