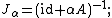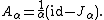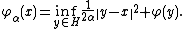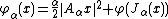1. Statement of the theorem

2. References

In mathematics, Moreau's theorem is a result in convex analysis. It shows that sufficiently well-behaved convex functionals on Hilbert spaces are differentiable and the derivative is well-approximated by the so-called Yosida approximation, which is defined in terms of the resolvent operator.

Statement of the theorem

Let H be a Hilbert space and let φ : H → R ∪ {+∞} be a proper, convex and lower semi-continuous extended real-valued functional on H. Let A stand for ∂φ, the subderivative of φ; for α > 0 let J_α denote the resolvent:

and let A_α denote the Yosida approximation to A:

For each α > 0 and x ∈ H, let

Then

and φ_α is convex and Fréchet differentiable with derivative dφ_α = A_α. Also, for each x ∈ H (pointwise), φ_α(x) converges upwards to φ(x) as α → 0.

References

• {{cite book

}} {{MathSciNet|id=1422252}} (Proposition IV.1.8)

• Callitris roei
• Callitris sulcata
• Callitris verrucosa
• Callitropsis arizonica
• Callitropsis macrocarpa
• Callitropsis pigmaea
• Call It Sleep
• Call It Stormy Monday
• Call It Stormy Monday (But Tuesday Is Just as Bad)
• Call It Stormy Monday (But Tuesday's Just As Bad)
• Callixalus
• Callixalus pictus
• Callixenus
• Callixenus (given name)
• Callixenus of Rhodes
• Callixte Gakwaya
• Callixte Nzabonimana
• Callixtus
• Call Lake Provincial Park
• Call letter
• Call Letters
• Call Liberty
• Call logging
• Call Me a Cabbie
• Call Me a Dog