- Definition
- Estimation
- Practical application of multifractal spectra DQ vs Q Dimensional ordering
 vs
vs  Generalized dimensions of species abundance distributions in space
Generalized dimensions of species abundance distributions in space - Estimating multifractal scaling from box counting
- Applications
- See also
- References
- External links
A multifractal system is a generalization of a fractal system in which a single exponent (the fractal dimension) is not enough to describe its dynamics; instead, a continuous spectrum of exponents (the so-called singularity spectrum) is needed.[1]
Multifractal systems are common in nature. They include the length of coastlines, fully developed turbulence, real world scenes, the Sun's magnetic field time series{{Citation needed|date=November 2018}}, heartbeat dynamics,[2] human gait{{Citation needed|date=November 2018}} and activity,[3] human brain activity,[4][5][6][7][8][9][10] and natural luminosity time series{{Citation needed|date=November 2018}}. Models have been proposed in various contexts ranging from turbulence in fluid dynamics to internet traffic, finance, image modeling, texture synthesis, meteorology, geophysics and more{{Citation needed|date=November 2018}}. The origin of multifractality in sequential (time series) data has been attributed to mathematical convergence effects related to the central limit theorem that have as foci of convergence the family of statistical distributions known as the Tweedie exponential dispersion models[11] as well as the geometric Tweedie models.[12] The first convergence effect yields monofractal sequences and the second convergence effect is responsible for variation in the fractal dimension of the monofractal sequences.[13]
Multifractal analysis uses mathematical basis to investigate datasets, often in conjunction with other methods of fractal analysis and lacunarity analysis. The technique entails distorting datasets extracted from patterns to generate multifractal spectra that illustrate how scaling varies over the dataset. Multifractal analysis techniques have been applied in a variety of practical situations such as predicting earthquakes and interpreting medical images.[14][15][16]
Definition
In a multifractal system  , the behavior around any point is described by a local power law:
, the behavior around any point is described by a local power law:
The exponent  is called the singularity exponent, as it describes the local degree of singularity or regularity around the point
is called the singularity exponent, as it describes the local degree of singularity or regularity around the point  .{{Citation needed|date=November 2018}}
.{{Citation needed|date=November 2018}}
The ensemble formed by all the points that share the same singularity exponent is called the singularity manifold of exponent h, and is a fractal set of fractal dimension  : the singularity spectrum. The curve
: the singularity spectrum. The curve  versus h is called the singularity spectrum and fully describes the (statistical) distribution of the variable
versus h is called the singularity spectrum and fully describes the (statistical) distribution of the variable  .{{Citation needed|date=November 2018}}
.{{Citation needed|date=November 2018}}
In practice, the multifractal behaviour of a physical system  is not directly characterized by its singularity spectrum
is not directly characterized by its singularity spectrum  . Data analysis rather gives access to the multiscaling exponents
. Data analysis rather gives access to the multiscaling exponents  . Indeed, multifractal signals generally obey a scale invariance property which yields power law behaviours for multiresolution quantities depending on their scale
. Indeed, multifractal signals generally obey a scale invariance property which yields power law behaviours for multiresolution quantities depending on their scale  . Depending on the object under study, these multiresolution quantities, denoted by
. Depending on the object under study, these multiresolution quantities, denoted by  in the following, can be local averages in boxes of size
in the following, can be local averages in boxes of size  , gradients over distance
, gradients over distance  , wavelet coefficients at scale
, wavelet coefficients at scale  ... For multifractal objects, one usually observes a global power law scaling of the form:{{Citation needed|date=November 2018}}
... For multifractal objects, one usually observes a global power law scaling of the form:{{Citation needed|date=November 2018}}
at least in some range of scales and for some range of orders  . When such a behaviour is observed, one talks of scale invariance, self-similarity or multiscaling.[17]
. When such a behaviour is observed, one talks of scale invariance, self-similarity or multiscaling.[17]
Estimation
Using the so-called multifractal formalism, it can be shown that, under some well-suited assumptions, there exists a correspondence between the singularity spectrum  and the multi scaling exponents
and the multi scaling exponents  through a Legendre transform. While the determination of
through a Legendre transform. While the determination of  calls for some exhaustive local analysis of the data, which would result in difficult and numerically unstable calculations, the estimation of the
calls for some exhaustive local analysis of the data, which would result in difficult and numerically unstable calculations, the estimation of the  relies on the use of statistical averages and linear regressions in log-log diagrams. Once the
relies on the use of statistical averages and linear regressions in log-log diagrams. Once the  are known, one can deduce an estimate of
are known, one can deduce an estimate of  thanks to a simple Legendre transform.{{Citation needed|date=November 2018}}
thanks to a simple Legendre transform.{{Citation needed|date=November 2018}}
Multifractal systems are often modeled by stochastic processes such as multiplicative cascades. The  receives some statistical interpretation as they characterize the evolution of the distributions of the
receives some statistical interpretation as they characterize the evolution of the distributions of the  as
as  goes from larger to smaller scales. This evolution is often called statistical intermittency and betrays a departure from Gaussian models.{{Citation needed|date=November 2018}}
goes from larger to smaller scales. This evolution is often called statistical intermittency and betrays a departure from Gaussian models.{{Citation needed|date=November 2018}}
Modelling as a multiplicative cascade also leads to estimation of multifractal properties ({{harvnb|Roberts|Cronin|1996}}). This methods works reasonably well even for relatively small datasets A maximum likelihood fit of a multiplicative cascade to the dataset not only estimates the complete spectrum, but also gives reasonable estimates of the errors (see the web service ).
{{anchor|techniques}}Practical application of multifractal spectra
{{anchor|distort}}Multifractal analysis has been used in several science fields to characterize various types of datasets.[18][3][6] In essence, multifractal analysis applies a distorting factor to datasets extracted from patterns, to compare how the data behave at each distortion. This is done using graphs known as multifractal spectra, analogous to viewing the dataset through a "distorting lens" as shown in the illustration.[21] Several types of multifractal spectra are used in practise.DQ vs Q
{{anchor|dqvsq}}{{anchor|dimensional ordering}}One practical multifractal spectrum is the graph of DQ vs Q, where DQ is the generalized dimension for a dataset and Q is an arbitrary set of exponents. The expression generalized dimension thus refers to a set of dimensions for a dataset (detailed calculations for determining the generalized dimension using box counting are described below).Dimensional ordering
The general pattern of the graph of DQ vs Q can be used to assess the scaling in a pattern. The graph is generally decreasing, sigmoidal around Q=0, where D(Q=0) ≥ D(Q=1) ≥ D(Q=2). As illustrated in the figure, variation in this graphical spectrum can help distinguish patterns. The image shows D(Q) spectra from a multifractal analysis of binary images of non-, mono-, and multi-fractal sets. As is the case in the sample images, non- and mono-fractals tend to have flatter D(Q) spectra than multifractals.
The generalized dimension also offers some important specific information. D(Q=0) is equal to the capacity dimension, which in the analysis shown in the figures here is the box counting dimension. D(Q=1) is equal to the information dimension, and D(Q=2) to the correlation dimension. This relates to the "multi" in multifractal whereby multifractals have multiple dimensions in the D(Q) vs Q spectra but monofractals stay rather flat in that area.[21][23]
 vs
vs 
Another useful multifractal spectrum is the graph of  vs
vs  (see calculations). These graphs generally rise to a maximum that approximates the fractal dimension at Q=0, and then fall. Like DQ vs Q spectra, they also show typical patterns useful for comparing non-, mono-, and multi-fractal patterns. In particular, for these spectra, non- and mono-fractals converge on certain values, whereas the spectra from multifractal patterns are typically humped over a broader extent.
(see calculations). These graphs generally rise to a maximum that approximates the fractal dimension at Q=0, and then fall. Like DQ vs Q spectra, they also show typical patterns useful for comparing non-, mono-, and multi-fractal patterns. In particular, for these spectra, non- and mono-fractals converge on certain values, whereas the spectra from multifractal patterns are typically humped over a broader extent.
Generalized dimensions of species abundance distributions in space
One application of Dq vs q in ecology is the characterization of the abundance distribution of species. Traditionally the relative species abundances is calculated for an area without taking into account the positions of the individuals. An equivalent representation of relative species abundances are species ranks, used to generate a surface called the species-rank surface,[19] which can be analyzed using generalized dimensions to detect different ecological mechanisms like the ones observed in neutral theory of biodiversity, metacommunity dynamics or niche theory.[19][20]
Estimating multifractal scaling from box counting
{{anchor|calculations}}Multifractal spectra can be determined from box counting on digital images. First, a box counting scan is done to determine how the pixels are distributed; then, this "mass distribution" becomes the basis for a series of calculations.[21][22][23] The chief idea is that for multifractals, the probability  of a number of pixels
of a number of pixels  , appearing in a box
, appearing in a box  , varies as box size
, varies as box size  , to some exponent
, to some exponent  , which changes over the image, as in {{EquationNote|Eq.0.0}}. NB: For monofractals, in contrast, the exponent does not change meaningfully over the set.
, which changes over the image, as in {{EquationNote|Eq.0.0}}. NB: For monofractals, in contrast, the exponent does not change meaningfully over the set.  is calculated from the box counting pixel distribution as in {{EquationNote|Eq.2.0}}.
is calculated from the box counting pixel distribution as in {{EquationNote|Eq.2.0}}.
 |{{EquationRef|Eq.0.0}}}}
|{{EquationRef|Eq.0.0}}}}= an arbitrary scale (box size in box counting) at which the set is examined
= the index for each box laid over the set for an
= the number of pixels or mass in any box,
, at size
{{NumBlk|:|= the total boxes that contained more than 0 pixels, for each
 the total mass or sum of pixels in all boxes for this
the total mass or sum of pixels in all boxes for this  |{{EquationRef|Eq.1.0}}}}{{NumBlk|:|
|{{EquationRef|Eq.1.0}}}}{{NumBlk|:| the probability of this mass at
the probability of this mass at  relative to the total mass for a box size|{{EquationRef|Eq.2.0}}}}
relative to the total mass for a box size|{{EquationRef|Eq.2.0}}}} is used to observe how the pixel distribution behaves when distorted in certain ways as in {{EquationNote|Eq.3.0}} and {{EquationNote|Eq.3.1}}:
is used to observe how the pixel distribution behaves when distorted in certain ways as in {{EquationNote|Eq.3.0}} and {{EquationNote|Eq.3.1}}:
{{NumBlk|:|= an arbitrary range of values to use as exponents for distorting the data set
 the sum of all mass probabilities distorted by being raised to this Q, for this box size|{{EquationRef |Eq.3.0}}}}
the sum of all mass probabilities distorted by being raised to this Q, for this box size|{{EquationRef |Eq.3.0}}}}- When
 , {{EquationNote|Eq.3.0}} equals 1, the usual sum of all probabilities, and when
, {{EquationNote|Eq.3.0}} equals 1, the usual sum of all probabilities, and when  , every term is equal to 1, so the sum is equal to the number of boxes counted,
, every term is equal to 1, so the sum is equal to the number of boxes counted,  .
.
 how the distorted mass probability at a box compares to the distorted sum over all boxes at this box size|{{EquationRef|Eq.3.1}}}}
how the distorted mass probability at a box compares to the distorted sum over all boxes at this box size|{{EquationRef|Eq.3.1}}}}These distorting equations are further used to address how the set behaves when scaled or resolved or cut up into a series of  -sized pieces and distorted by Q, to find different values for the dimension of the set, as in the following:
-sized pieces and distorted by Q, to find different values for the dimension of the set, as in the following:
- An important feature of {{EquationNote|Eq.3.0}} is that it can also be seen to vary according to scale raised to the exponent
 in {{EquationNote|Eq.4.0}}:
in {{EquationNote|Eq.4.0}}:
 |{{EquationRef|Eq.4.0}}}}
|{{EquationRef|Eq.4.0}}}}Thus, a series of values for  can be found from the slopes of the regression line for the log of {{EquationNote|Eq.3.0}} versus the log of
can be found from the slopes of the regression line for the log of {{EquationNote|Eq.3.0}} versus the log of  for each
for each  , based on {{EquationNote|Eq.4.1}}:
, based on {{EquationNote|Eq.4.1}}:
 |{{EquationRef|Eq.4.1}}}}
|{{EquationRef|Eq.4.1}}}}- {{anchor|generalized dimension}}For the generalized dimension:
 |{{EquationRef|Eq.5.0}}}}{{NumBlk|:|
|{{EquationRef|Eq.5.0}}}}{{NumBlk|:| |{{EquationRef|Eq.5.1}}}}{{NumBlk|:|
|{{EquationRef|Eq.5.1}}}}{{NumBlk|:| |{{EquationRef|Eq.5.2}}}}{{NumBlk|:|
|{{EquationRef|Eq.5.2}}}}{{NumBlk|:| |{{EquationRef|Eq.5.3}}}}
|{{EquationRef|Eq.5.3}}}}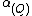 is estimated as the slope of the regression line for {{math|log A
is estimated as the slope of the regression line for {{math|log A ,Q}} versus {{math|log
,Q}} versus {{math|log  }} where:
}} where:
 |{{EquationRef|Eq.6.0}}}}
|{{EquationRef|Eq.6.0}}}}- Then
 is found from {{EquationNote|Eq.5.3}}.
is found from {{EquationNote|Eq.5.3}}.
- The mean
 is estimated as the slope of the log-log regression line for
is estimated as the slope of the log-log regression line for  versus
versus  , where:
, where:
 |{{EquationRef|Eq.6.1}}}}
|{{EquationRef|Eq.6.1}}}}In practice, the probability distribution depends on how the dataset is sampled, so optimizing algorithms have been developed to ensure adequate sampling.[21]
Applications
Multifractal analysis has been successfully used in many fields including biology and physical sciences.[24] For example, the quantification of residual crack patterns on the surface of reinforced concrete shear walls.[25]
See also
- Multifractal Model of Asset Returns (MMAR)
- Multifractal Random Walk model (MRW)
- Fractional Brownian motion
- Mandelbrot cascade, continuous cascade and lognormal cascade
- Detrended fluctuation analysis
- Tweedie distributions
- Markov switching multifractal
- Weighted planar stochastic lattice (WPSL) [26]
References
2. ^{{Cite journal|last=Ivanov|first=Plamen Ch.|last2=Amaral|first2=Luís A. Nunes|last3=Goldberger|first3=Ary L.|last4=Havlin|first4=Shlomo|last5=Rosenblum|first5=Michael G.|last6=Struzik|first6=Zbigniew R.|last7=Stanley|first7=H. Eugene|date=1999-06-03|title=Multifractality in human heartbeat dynamics|url=https://www.nature.com/articles/20924|journal=Nature|language=En|volume=399|issue=6735|pages=461–465|doi=10.1038/20924|pmid=10365957|issn=0028-0836|arxiv=cond-mat/9905329}}
3. ^1 {{Cite journal|last=França|first=Lucas Gabriel Souza|last2=Montoya|first2=Pedro|last3=Miranda|first3=José Garcia Vivas|date=2019|title=On multifractals: A non-linear study of actigraphy data|url=https://linkinghub.elsevier.com/retrieve/pii/S037843711831255X|journal=Physica A: Statistical Mechanics and its Applications|volume=514|pages=612–619|doi=10.1016/j.physa.2018.09.122|issn=0378-4371|via=|arxiv=1702.03912}}
4. ^{{Cite journal|last=Papo|first=David|last2=Goñi|first2=Joaquin|last3=Buldú|first3=Javier M.|date=2017|title=Editorial: On the relation of dynamics and structure in brain networks|journal=Chaos: An Interdisciplinary Journal of Nonlinear Science|language=en|volume=27|issue=4|pages=047201|doi=10.1063/1.4981391|pmid=28456177|issn=1054-1500}}
5. ^{{Cite journal|last=Ciuciu|first=Philippe|last2=Varoquaux|first2=Gaël|last3=Abry|first3=Patrice|last4=Sadaghiani|first4=Sepideh|last5=Kleinschmidt|first5=Andreas|date=2012|title=Scale-free and multifractal properties of fMRI signals during rest and task|journal=Frontiers in Physiology|language=English|volume=3|pages=186|doi=10.3389/fphys.2012.00186|issn=1664-042X|pmc=3375626|pmid=22715328}}
6. ^1 {{Cite journal|last=França|first=Lucas G. Souza|last2=Miranda|first2=José G. Vivas|last3=Leite|first3=Marco|last4=Sharma|first4=Niraj K.|last5=Walker|first5=Matthew C.|last6=Lemieux|first6=Louis|last7=Wang|first7=Yujiang|date=2018|title=Fractal and Multifractal Properties of Electrographic Recordings of Human Brain Activity: Toward Its Use as a Signal Feature for Machine Learning in Clinical Applications|journal=Frontiers in Physiology|language=English|volume=9|pages=1767|doi=10.3389/fphys.2018.01767|pmid=30618789|pmc=6295567|issn=1664-042X}}
7. ^{{Cite journal|last=Ihlen|first=Espen A. F.|last2=Vereijken|first2=Beatrix|date=2010|title=Interaction-dominant dynamics in human cognition: Beyond 1/ƒα fluctuation.|journal=Journal of Experimental Psychology: General|language=en|volume=139|issue=3|pages=436–463|doi=10.1037/a0019098|pmid=20677894|issn=1939-2222}}
8. ^{{Cite journal|last=Zhang|first=Yanli|last2=Zhou|first2=Weidong|last3=Yuan|first3=Shasha|date=2015|title=Multifractal Analysis and Relevance Vector Machine-Based Automatic Seizure Detection in Intracranial EEG|journal=International Journal of Neural Systems|language=en|volume=25|issue=6|pages=1550020|doi=10.1142/s0129065715500203|pmid=25986754|issn=0129-0657}}
9. ^{{Cite journal|last=Suckling|first=John|last2=Wink|first2=Alle Meije|last3=Bernard|first3=Frederic A.|last4=Barnes|first4=Anna|last5=Bullmore|first5=Edward|date=2008|title=Endogenous multifractal brain dynamics are modulated by age, cholinergic blockade and cognitive performance|url=https://linkinghub.elsevier.com/retrieve/pii/S0165027008003841|journal=Journal of Neuroscience Methods|volume=174|issue=2|pages=292–300|doi=10.1016/j.jneumeth.2008.06.037|issn=0165-0270|pmc=2590659|pmid=18703089|via=}}
10. ^{{Cite journal|last=Zorick|first=Todd|last2=Mandelkern|first2=Mark A.|date=2013-07-03|title=Multifractal Detrended Fluctuation Analysis of Human EEG: Preliminary Investigation and Comparison with the Wavelet Transform Modulus Maxima Technique|journal=PLoS ONE|language=en|volume=8|issue=7|pages=e68360|doi=10.1371/journal.pone.0068360|issn=1932-6203|pmc=3700954|pmid=23844189}}
11. ^{{cite journal | last1 = Kendal | first1 = WS | last2 = Jørgensen | first2 = BR | year = 2011 | title = Tweedie convergence: a mathematical basis for Taylor's power law, 1/f noise and multifractality | url = | journal = Phys. Rev. E | volume = 84 | issue = 6 Pt 2| page = 066120 | doi=10.1103/physreve.84.066120 | pmid=22304168| bibcode = 2011PhRvE..84f6120K }}
12. ^{{cite journal | last1 = Jørgensen | first1 = B | last2 = Kokonendji | first2 = CC | year = 2011 | title = Dispersion models for geometric sums | url = | journal = Braz J Probab Stat | volume = 25 | issue = 3| pages = 263–293 | doi=10.1214/10-bjps136}}
13. ^{{cite journal | last1 = Kendal | first1 = WS | year = 2014 | title = Multifractality attributed to dual central limit-like convergence effects | url = | journal = Physica A | volume = 401 | issue = | pages = 22–33 | doi=10.1016/j.physa.2014.01.022| bibcode = 2014PhyA..401...22K}}
14. ^{{Cite journal | last1 = Lopes | first1 = R. | last2 = Betrouni | first2 = N. | doi = 10.1016/j.media.2009.05.003 | title = Fractal and multifractal analysis: A review | journal = Medical Image Analysis | volume = 13 | issue = 4 | pages = 634–649 | year = 2009 | pmid = 19535282 | pmc = }}
15. ^{{Cite journal | last1 = Moreno | first1 = P. A. | last2 = Vélez | first2 = P. E. | last3 = Martínez | first3 = E. | last4 = Garreta | first4 = L. E. | last5 = Díaz | first5 = N. S. | last6 = Amador | first6 = S. | last7 = Tischer | first7 = I. | last8 = Gutiérrez | first8 = J. M. | last9 = Naik | first9 = A. K. | last10 = Tobar | first10 = F. N. | last11 = García | first11 = F. | title = The human genome: A multifractal analysis | doi = 10.1186/1471-2164-12-506 | journal = BMC Genomics | volume = 12 | pages = 506 | year = 2011 | pmid = 21999602| pmc =3277318 }}
16. ^{{Cite journal | last1 = Atupelage | first1 = C. | last2 = Nagahashi | first2 = H. | last3 = Yamaguchi | first3 = M. | last4 = Sakamoto | first4 = M. | last5 = Hashiguchi | first5 = A. | title = Multifractal feature descriptor for histopathology | journal = Analytical Cellular Pathology | volume = 35 | issue = 2 | pages = 123–126 | doi = 10.3233/ACP-2011-0045 | year = 2012 | pmid = 22101185 | pmc = 4605731}}
17. ^{{cite journal |author=A.J. Roberts and A. Cronin |title=Unbiased estimation of multi-fractal dimensions of finite data sets |journal=Physica A |volume=233 |issue=3 |year=1996 |pages=867–878 |doi=10.1016/S0378-4371(96)00165-3 |arxiv=chao-dyn/9601019 |bibcode=1996PhyA..233..867R }}
18. ^{{Cite journal | last1 = Trevino | first1 = J. | last2 = Liew | first2 = S. F. | last3 = Noh | first3 = H. | last4 = Cao | first4 = H. | last5 = Dal Negro | first5 = L. | title = Geometrical structure, multifractal spectra and localized optical modes of aperiodic Vogel spirals | doi = 10.1364/OE.20.003015 | journal = Optics Express | volume = 20 | issue = 3 | pages = 3015 | year = 2012 | pmid = | pmc = | bibcode = 2012OExpr..20.3015T }}
19. ^1 {{Cite journal|last=Saravia|first=Leonardo A.|date=2015-08-01|title=A new method to analyse species abundances in space using generalized dimensions|url=https://peerj.com/preprints/745v5/|journal=Methods in Ecology and Evolution|volume=6|issue=11|pages=1298–1310|doi=10.1111/2041-210X.12417|issn=2041-210X}}
20. ^{{Cite journal|title = mfSBA: Multifractal analysis of spatial patterns in ecological communities|url = http://f1000research.com/articles/3-14/v2|journal = F1000Research|date = 2014-01-01|pmc = 4197745|pmid = 25324962|doi = 10.12688/f1000research.3-14.v2|first = Leonardo A.|last = Saravia|volume=3|pages=14}}
21. ^1 2 3 {{citation |author=Karperien, A |title=What are Multifractals? |publisher=ImageJ |accessdate=2012-02-10 |url=http://rsbweb.nih.gov/ij/plugins/fraclac/FLHelp/Multifractals.htm |year=2002 |archiveurl=https://www.webcitation.org/65LENzkV8?url=http://rsbweb.nih.gov/ij/plugins/fraclac/FLHelp/Multifractals.htm |archivedate=2012-02-10 |deadurl=no |df= }}
22. ^1 {{Cite journal | last1 = Chhabra | first1 = A. | last2 = Jensen | first2 = R. | doi = 10.1103/PhysRevLett.62.1327 | title = Direct determination of the f(α) singularity spectrum | journal = Physical Review Letters | volume = 62 | issue = 12 | pages = 1327–1330 | year = 1989 | pmid = 10039645| pmc = |bibcode = 1989PhRvL..62.1327C }}
23. ^{{Cite journal | last1 = Posadas | first1 = A. N. D. | last2 = Giménez | first2 = D. | last3 = Bittelli | first3 = M. | last4 = Vaz | first4 = C. M. P. | last5 = Flury | first5 = M. | title = Multifractal Characterization of Soil Particle-Size Distributions | doi = 10.2136/sssaj2001.6551361x | journal = Soil Science Society of America Journal | volume = 65 | issue = 5 | pages = 1361 | year = 2001 | pmid = | pmc = | bibcode = 2001SSASJ..65.1361P }}
24. ^{{Cite journal|date=2009|title=Fractal and multifractal analysis: A review|journal=Medical Image Analysis|volume=13|issue=4|pages=634–649|doi=10.1016/j.media.2009.05.003|pmid=19535282|last1=Lopes|first1=R.|last2=Betrouni|first2=N.}}
25. ^{{Cite journal|last=Ebrahimkhanlou|first=Arvin|last2=Farhidzadeh|first2=Alireza|last3=Salamone|first3=Salvatore|date=2016-01-01|title=Multifractal analysis of crack patterns in reinforced concrete shear walls|journal=Structural Health Monitoring|language=en|volume=15|issue=1|pages=81–92|doi=10.1177/1475921715624502|issn=1475-9217}}
26. ^{{cite journal | last1 = Hassan | first1 = M. K. | last2 = Hassan | first2 = M. Z. | last3 = Pavel | first3 = N. I. | year = 2010| title = Scale-free network topology and multifractality in a weighted planar stochastic lattice | url = | journal = New Journal of Physics | volume = 12 | issue = 9| page = 093045 | doi = 10.1088/1367-2630/12/9/093045 | arxiv = 1008.4994 | bibcode = 2010NJPh...12i3045H }}
{{cite journal |title=Flow through porous media with multifractal hydraulic conductivity |date=June 1, 2003 |issn=1944-7973 |doi=10.1029/2001WR001018 |issue=6 |pages = 1166|volume=39 |journal=Water Resources Research |first1=Daniele |last1=Veneziano |first2=Albert K. |last2=Essiam |bibcode=2003WRR....39.1166V}}
External links
- {{cite journal |author=Stanley H.E., Meakin P. |title=Multifractal phenomena in physics and chemistry |journal=Nature |volume=335 |year=1988 |pages=405–9 |url=http://polymer.bu.edu/hes/articles/sm88.pdf |format=Review |doi=10.1038/335405a0 |issue=6189|bibcode=1988Natur.335..405S }}
- {{cite journal |first1=Alain |last1=Arneodo |first2=Benjamin |last2=Audit |first3=Pierre |last3=Kestener |first4=Stephane |last4=Roux |title=Wavelet-based multifractal analysis |journal=Scholarpedia |volume=3 |issue=3 |pages=4103 |year=2008 |url=http://www.scholarpedia.org/article/Wavelet-based_multifractal_analysis |doi=10.4249/scholarpedia.4103|issn=1941-6016|bibcode=2008SchpJ...3.4103A }}
- Movies of visualizations of multifractals
- Zoran Ðindic
- Zoran Đorđević (football manager)
- Zoran Žigić
- Zoran Živkovic
- Zoran Živković (handballer)
- Zoran Žižić
- Zora Petrovic
- Zoras
- Zora Singh Maan
- Zora Sourit
- Zora sourit
- Zorastarian
- Zorastarianism
- Zorastarians
- Zoraster
- Zorastrian
- Zorastrianism
- Zorastrians
- Zoratama
- Zorats Karer
- Zoravan Yeghvard
- Zoravan Yegvard
- Zoravan Yegvart
- Zorawar Chand Bakhshi
- Zorawar Chand Bakshi

