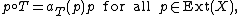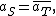“Multipliers and centralizers (Banach spaces)”的意思、由来-开放百科全书

词条

Multipliers and centralizers (Banach spaces)

释义

Definitions
Properties
References

In mathematics, multipliers and centralizers are algebraic objects in the study of Banach spaces. They are used, for example, in generalizations of the Banach-Stone theorem.

Definitions

Let (X, ‖·‖) be a Banach space over a field K (either the real or complex numbers), and let Ext(X) be the set of extreme points of the closed unit ball of the continuous dual space X^∗.

A continuous linear operator T : X → X is said to be a multiplier if every point p in Ext(X) is an eigenvector for the adjoint operator T^∗ : X^∗ → X^∗. That is, there exists a function a_T : Ext(X) → K such that

making the eigenvalue corresponding to p. Given two multipliers S and T on X, S is said to be an adjoint for T if

i.e. a_S agrees with a_T in the real case, and with the complex conjugate of a_T in the complex case.

The centralizer of X, denoted Z(X), is the set of all multipliers on X for which an adjoint exists.

Properties

The multiplier adjoint of a multiplier T, if it exists, is unique; the unique adjoint of T is denoted T^∗.
If the field K is the real numbers, then every multiplier on X lies in the centralizer of X.

References

{{cite journal

}} {{MathSciNet|id=2242851}}

2 : Banach spaces|Operator theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。