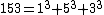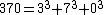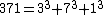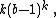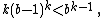1. Definition

2. Narcissistic numbers in various bases

3. Related concepts

4. References

5. External links

In recreational number theory, a narcissistic number^[1][2] (also known as a pluperfect digital invariant (PPDI),^[3] an Armstrong number^[4] (after Michael F. Armstrong)^[5] or a plus perfect number)^[6] is a number that is the sum of its own digits each raised to the power of the number of digits. This definition depends on the base b of the number system used, e.g., b = 10 for the decimal system or b = 2 for the binary system.

Definition

The definition of a narcissistic number relies on the decimal representation n = d_kd_k-1...d₁ of a natural number n, i.e.,

n = d_k·10^k-1 + d_k-1·10^k-2 + ... + d₂·10 + d₁,

with k digits d_i satisfying 0 ≤ d_i ≤ 9. Such a number n is called narcissistic if it satisfies the condition

n = d_k^k + d_k-1^k + ... + d₂^k + d₁^k.

For example, the 3-digit decimal number 153 is a narcissistic number because 153 = 1³ + 5³ + 3³.

Narcissistic numbers can also be defined with respect to numeral systems with a base b other than b = 10. The base-b representation of a natural number n is defined by

n = d_kb^k-1 + d_k-1b^k-2 + ... + d₂b + d₁,

where the base-b digits d_i satisfy the condition 0 ≤ d_i ≤ b-1.

For example, the (decimal) number 17 is a narcissistic number with respect to the numeral system with base b = 3. Its three base-3 digits are 122, because 17 = 1·3² + 2·3 + 2 , and it satisfies the equation 17 = 1³ + 2³ + 2³.

If the constraint that the power must equal the number of digits is dropped, so that for some m possibly different from k it happens that

n = d_k^m + d_k-1^m + ... + d₂^m + d₁^m,

then n is called a perfect digital invariant or PDI.^[2][7] For example, the decimal number 4150 has four decimal digits and is the sum of the fifth powers of its decimal digits

4150 = 4⁵ + 1⁵ + 5⁵ + 0⁵,

so it is a perfect digital invariant but not a narcissistic number.

In "A Mathematician's Apology", G. H. Hardy wrote:

There are just four numbers, after unity, which are the sums of the cubes of their digits:

.

These are odd facts, very suitable for puzzle columns and likely to amuse amateurs, but there is nothing in them which appeals to the mathematician.

Narcissistic numbers in various bases

The sequence of base 10 narcissistic numbers starts:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407, 1634, 8208, 9474, ... {{OEIS|id=A005188}}

The sequence of base 8 narcissistic numbers starts:

0, 1, 2, 3, 4, 5, 6, 7, 24, 64, 134, 205, 463, 660, 661, ... (sequence {{OEIS link|id=A010354}} and {{OEIS link|id=A010351}} in OEIS)

The sequence of base 12 narcissistic numbers starts:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ᘔ, Ɛ, 25, ᘔ5, 577, 668, ᘔ83, ... {{OEIS|id=A161949}}

The sequence of base 16 narcissistic numbers starts:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 156, 173, 208, 248, 285, 4A5, 5B0, 5B1, 60B, 64B, ... {{OEIS|id=A161953}}

The sequence of base 3 narcissistic numbers starts:

The sequence of base 4 narcissistic numbers starts:

0, 1, 2, 3, 130, 131, 203, 223, 313, 332, 1103, 3303 (sequence {{OEIS link|id=A010344}} and {{OEIS link|id=A010343}} in OEIS)

In base 2, the only narcissistic numbers are 0 and 1.

The number of narcissistic numbers in a given base is finite, since the maximum possible sum of the kth powers of a k digit number in base b is

and if k is large enough then

in which case no base b narcissistic number can have k or more digits. Setting b equal to 10 shows that the largest narcissistic number in base 10 must be less than 10⁶⁰.^[1]

There are only 88 narcissistic numbers in base 10, of which the largest is

115,132,219,018,763,992,565,095,597,973,971,522,401

with 39 digits.^[1]

Clearly, in all bases, all one-digit numbers are narcissistic numbers.

A base b has at least one two-digit narcissistic number if and only if b² + 1 is not prime, and the number of two-digit narcissistic numbers in base b equals 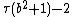, where 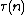is the number of positive divisors of n.

Every base b ≥ 3 that is not a multiple of nine has at least one three-digit narcissistic number. The bases that do not are

2, 72, 90, 108, 153, 270, 423, 450, 531, 558, 630, 648, 738, 1044, 1098, 1125, 1224, 1242, 1287, 1440, 1503, 1566, 1611, 1620, 1800, 1935, ... {{OEIS|id=A248970}}

Unlike narcissistic numbers, no upper bound can be determined for the size of PDIs in a given base, and it is not currently known whether or not the number of PDIs for an arbitrary base is finite or infinite.^[2]

Related concepts

The term "narcissistic number" is sometimes used in a wider sense to mean a number that is equal to any mathematical manipulation of its own digits. With this wider definition narcisstic numbers include:

• Constant base numbers : 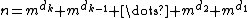for some m.
• Perfect digit-to-digit invariants or Münchhausen numbers {{OEIS|id=A046253}} : :
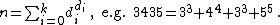
• Ascending power numbers {{OEIS|id=A032799}} :
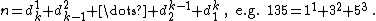
• Friedman numbers {{OEIS|id=A036057}}.
• Radical narcissistic numbers {{OEIS|id= A119710}} ^[8]
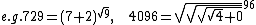
• Sum-product numbers {{OEIS|id=A038369}} :
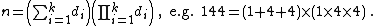
• Dudeney numbers {{OEIS|id=A061209}} :
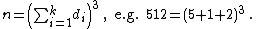
• Factorions {{OEIS|id=A014080}} :

where d_i are the digits of n in some base.

• Fresnillense numbers {{OEIS|id=A240511}} :
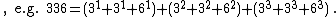
• Numbers n that are equal to a product of powers of digits where the exponents from left to right decrease with 1 and the exponent for the units digit is 1 (There are no other terms up to 10^200; this list is probably complete). {{OEIS|id=A282782}} :
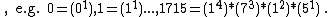
• Numbers n such that n = (sum of digits of n)((sum of digits of n) + 1) (the sequence is finite and full). {{OEIS|id=A282693}} :

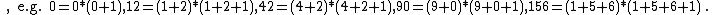
References

• Joseph S. Madachy, Mathematics on Vacation, Thomas Nelson & Sons Ltd. 1966, pages 163-175.
• Rose, Colin (2005), Radical narcissistic numbers, Journal of Recreational Mathematics, 33(4), 2004-2005, pages 250-254.
• [https://web.archive.org/web/20040606020332/http://mathews-archive.com/digit-related-numbers/pdi.html Perfect Digital Invariants] by Walter Schneider

External links

• Digital Invariants
• Armstrong Numbers
• [https://web.archive.org/web/20100109234250/http://ftp.cwi.nl/dik/Armstrong Armstrong Numbers in base 2 to 16]
• Armstrong numbers between 1-999 calculator
• {{cite web|last=Symonds|first=Ria|title=153 ♥ Narcissistic Number|url=http://www.numberphile.com/videos/153_narcissistic.html|work=Numberphile|publisher=Brady Haran}}

• Georg Jakob Felsing
• Georg Jann
• Georg Janny
• Georg Jauss
• Georg Joachim Zollikofer
• Georg Johan De Besche
• Georg Johannes von Trapp
• Georg Johansson
• Georg Johansson (footballer)
• Georg John Lober
• Georg Josef Riedel
• Georg Josef Wilhelm Aloys Rinck von Baldenstein
• Georg Joye
• Georg Jurii Nikolaewitch Woronow
• Georg Jurij Nikolaewitch Woronow
• Georg Karl Ignaz von Fechenbach zu Laudenbach
• Georg Kauffmann
• Georg Kenzian
• Georg Kesler
• Georg K. Glaser
• Georg Kiessling
• Georg Kießling
• Georg Klein
• Georg Klein (biologist)
• Georg Klein (disambiguation)