- See also
- References
In mathematics, a nonhypotenuse number is a natural number whose square cannot be written as the sum of two nonzero squares. The name stems from the fact that an edge of length equal to a nonhypotenuse number cannot form the hypotenuse of a right angle triangle with integer sides.
The numbers 1, 2, 3 and 4 are all nonhypotenuse numbers. The number 5, however, is not a nonhypotenuse number as 52 equals 32 + 42.
The first fifty nonhypotenuse numbers are:
1, 2, 3, 4, 6, 7, 8, 9, 11, 12, 14, 16, 18, 19, 21, 22, 23, 24, 27, 28, 31, 32, 33, 36, 38, 42, 43, 44, 46, 47, 48, 49, 54, 56, 57, 59, 62, 63, 64, 66, 67, 69, 71, 72, 76, 77, 79, 81, 83, 84 {{OEIS|id=A004144}}
Although nonhypotenuse numbers are common among small integers, they become more-and-more sparse for larger numbers. Yet, there are infinitely many nonhypotenuse numbers, and the number of nonhypotenuse numbers not exceeding a value x scales asymptotically with x/{{radic|log x}}.[1]
The nonhypotenuse numbers are those numbers that have no prime factors of the form 4k+1.[2] Equivalently, any number that cannot be put into the form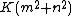 
where K, m, and n are all positive integers, is never a nonhypotenuse number. A number whose prime factors are not {{em|all}} of the form 4k+1 cannot be the hypotenuse of a primitive triangle, but may still be the hypotenuse of a non-primitive triangle.[3]
See also
- Nonhypotenuse Numbers {{OEIS|id=A004144}}
- Eta Numbers {{OEIS|id=A125667}}
- Pythagorean theorem
- Landau-Ramanujan constant
- Fermat's theorem on sums of two squares
References
2. ^{{citation|first=D.|last=Shanks|authorlink=Daniel Shanks|title=Non-hypotenuse numbers|journal=Fibonacci Quarterly|volume=13|issue=4|year=1975|pages=319–321|mr=0387219}}.
3. ^{{cite book|last1=Beiler|first1=Albert|title=Recreations in the Theory of Numbers: The Queen of Mathematics Entertains|date=1966|publisher=Dover Publications|location=New York|isbn=978-0-486-21096-4|page=116-117|edition=2}}
- Trophon bonneti
- Trophon brevispira
- Trophon clenchi
- Trophon columnaris
- Trophon condensatus
- Trophon convexus
- Trophon coulmanensis
- Trophon crispus
- Trophon cuspidarioides
- Trophon dispar
- Trophon distantelamellatus
- Trophon drygalskii
- Trophon dubius
- Trophon echinolamellatus
- Trophonella
- Trophonella echinolamellata
- Trophonella enderbyensis
- Trophonella eversoni
- Trophonella longstaffi
- Trophonella scotiana
- Trophonella shackletoni
- Trophon emilyae
- Trophon enderbyensis
- Trophon erectus
- Trophon eversoni