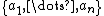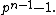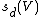- Examples
- References
- External links
In mathematics, a norm variety is a particular type of algebraic variety V over a field F, introduced for the purposes of algebraic K-theory by Voevodsky. The idea is to relate Milnor K-theory of F to geometric objects V, having function fields F(V) that 'split' given 'symbols' (elements of Milnor K-groups).[1]
The formulation is that p is a given prime number, different from the characteristic of F, and a symbol is the class mod p of an element
of the n-th Milnor K-group. A field extension is said to split the symbol, if its image in the K-group for that field is 0.
The conditions on a norm variety V are that V is irreducible and a non-singular complete variety. Further it should have dimension d equal to
The key condition is in terms of the d-th Newton polynomial sd, evaluated on the (algebraic) total Chern class of the tangent bundle of V. This number
should not be divisible by p2, it being known it is divisible by p.
Examples
These include (n = 2) cases of the Severi–Brauer variety and (p = 2) Pfister forms. There is an existence theorem in the general case (paper of Markus Rost cited).
References
External links
- Paper by Rost
- Ideal gas laws
- Ideal german
- Ideal (German band)
- Ideal German campaign
- Ideal Home
- Ideal Home Exhibitions
- Idealised love
- Idealism (album)
- Idealism (Christian eschatology)
- Idealism in international relations theory
- Idealistic pluralism
- Idealist on Campus
- Idealist.org
- Idealist temperament
- Idealization and devaluation
- Idealized love
- Ideal Jawa
- Ideal (Lie algebra)
- Ideally hard superconductor
- Ideal mental health
- Ideal Mini
- Ideal Mini School
- Ideal mixture
- Idealno loša
- Idealno Tvoja