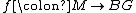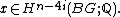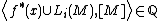“Novikov conjecture”的意思、由来-开放百科全书

词条

Novikov conjecture

释义

Precise formulation of the conjecture
Connection with the Borel conjecture
References
External links

This page concerns mathematician Sergei Novikov's topology conjecture. For astrophysicist Igor Novikov's conjecture regarding time travel, see Novikov self-consistency principle.

The Novikov conjecture is one of the most important unsolved problems in topology. It is named for Sergei Novikov who originally posed the conjecture in 1965.

The Novikov conjecture concerns the homotopy invariance of certain polynomials in the Pontryagin classes of a manifold, arising from the fundamental group. According to the Novikov conjecture, the higher signatures, which are certain numerical invariants of smooth manifolds, are homotopy invariants.

The conjecture has been proved for finitely generated abelian groups. It is not yet known whether the Novikov conjecture holds true for all groups. There are no known counterexamples to the conjecture.

Precise formulation of the conjecture

Let be a discrete group and its classifying space, which is a Eilenberg–MacLane space of type 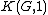, and therefore unique up to homotopy equivalence as a CW complex. Let

be a continuous map from a closed oriented -dimensional manifold to , and

Novikov considered the numerical expression, found by evaluating the cohomology class in top dimension against the fundamental class , and known as a higher signature:

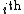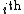
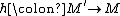where is the Hirzebruch polynomial, or sometimes (less descriptively) as the -polynomial. For each , this polynomial can be expressed in the Pontryagin classes of the manifold's tangent bundle. The Novikov conjecture states that the higher signature is an invariant of the oriented homotopy type of for every such map and every such class , in other words, if is an orientation preserving homotopy equivalence, the higher signature associated to 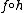is equal to that associated to .

Connection with the Borel conjecture

The Novikov conjecture is equivalent to the rational injectivity of the assembly map in L-theory. The

Borel conjecture on the rigidity of aspherical manifolds is equivalent to the assembly map being an isomorphism.

References

{{Citation | last1=Davis | first1=James F. | editor1-last=Cappell | editor1-first=Sylvain | editor1-link=Sylvain Cappell|editor2-last=Ranicki | editor2-first=Andrew | editor2-link=Andrew Ranicki|editor3-last=Rosenberg | editor3-first=Jonathan | editorlink3=Jonathan Rosenberg (mathematician) | title=Surveys on surgery theory. Vol. 1 | url=http://www.indiana.edu/~jfdavis/papers/d_manc.pdf | publisher=Princeton University Press | series=Annals of Mathematics Studies | isbn=978-0-691-04937-3|mr=1747536 | year=2000 | chapter=Manifold aspects of the Novikov conjecture | pages=195–224}}
John Milnor and James D. Stasheff, Characteristic Classes, Annals of Mathematics Studies 76, Princeton (1974).
Sergei P. Novikov, Algebraic construction and properties of Hermitian analogs of k-theory over rings with involution from the point of view of Hamiltonian formalism. Some applications to differential topology and to the theory of characteristic classes. Izv.Akad.Nauk SSSR, v. 34, 1970 I N2, pp. 253–288; II: N3, pp. 475–500. English summary in Actes Congr. Intern. Math., v. 2, 1970, pp. 39–45.

External links

Biography of Sergei Novikov
Novikov Conjecture Bibliography
Novikov Conjecture 1993 Oberwolfach Conference Proceedings, Volume 1
Novikov Conjecture 1993 Oberwolfach Conference Proceedings, Volume 2
2004 Oberwolfach Seminar notes on the Novikov Conjecture (pdf)
Scholarpedia article by S.P. Novikov (2010)
The Novikov Conjecture at the Manifold Atlas

4 : Geometric topology|Homotopy theory|Conjectures|Surgery theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。