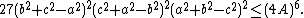- Statement of the inequality
- See also
- References
- External links
In mathematics, Ono's inequality is a theorem about triangles in the Euclidean plane. In its original form, as conjectured by T. Ono in 1914, the inequality is actually false; however, the statement is true for acute triangles and right triangles, as shown by F. Balitrand in 1916.
Statement of the inequality
Consider an acute or right triangle in the Euclidean plane with side lengths a, b and c and area A. Then
This inequality fails for general triangles (to which Ono's original conjecture applied), as shown by the counterexample 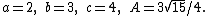
The inequality holds with equality in the case of an equilateral triangle, in which up to similarity we have sides 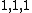 and area
and area 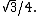
See also
- List of triangle inequalities
References
- {{cite journal
| last = Balitrand
| first = F.
| title = Problem 4417
| journal = Intermed. Math.
| volume = 23
| pages = 86–87
| year = 1916
| JFM = 46.0859.06
}}
- {{cite journal
| last = Ono
| first = T.
| title = Problem 4417
| journal = Intermed. Math.
| volume = 21
| pages = 146
| year = 1914
}}
- {{cite journal
| last = Quijano
| first = G.
| title = Problem 4417
| journal = Intermed. Math.
| volume = 22
| pages = 66
| year = 1915
}}
External links
- {{MathWorld|urlname=OnoInequality|title=Ono inequality}}
3 : Disproved conjectures|Triangle geometry|Geometric inequalities
- 7th St / Metro Center station
- 7th Streamy Awards
- 7th Street and Jones station
- 7th Street Casino
- 7th Street-Convention Center station
- 7th Street-Convention Center station (Washington, D.C.)
- 7th Street-Convention Center station (Washington Metro)
- 7th Street Depot (Louisville)
- 7th Street (Lynx station)
- 7th Street/Metro Center (Los Angeles Metro station)
- 7th Street / Metro Center station
- 7th Street / Metro Center station (Los Angeles Metro)
- 7th Street/Metro Center station (Los Angeles Metro)
- 7th Street Pike
- 7th Street station
- 7th Street station (Charlotte, North Carolina)
- 7th Street station (disambiguation)
- 7th Street station (Los Angeles Metro)
- 7th Street–Convention Center station
- 7th Street–Convention Center station (Washington, D.C.)
- 7th Street–Convention Center station (Washington Metro)
- 7th Support Group
- 7th Tarang Cine Awards
- 7th TVyNovelas Awards
- 7th United Kingdom general election