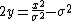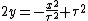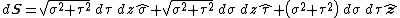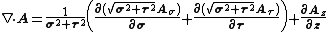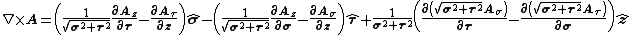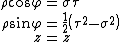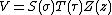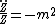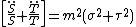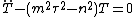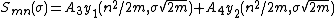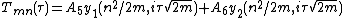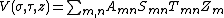“Parabolic cylindrical coordinates”的意思、由来-开放百科全书

词条

Parabolic cylindrical coordinates

释义

Basic definition
Scale factors
Differential elements
Del
Relationship to other coordinate systems
Parabolic cylinder harmonics
Applications
See also
Bibliography
External links

In mathematics, parabolic cylindrical coordinates are a three-dimensional orthogonal coordinate system that results from projecting the two-dimensional parabolic coordinate system in the

perpendicular -direction. Hence, the coordinate surfaces are confocal parabolic cylinders. Parabolic cylindrical coordinates have found many applications, e.g., the potential theory of edges.

Basic definition

The parabolic cylindrical coordinates {{math|(σ, τ, z)}} are defined in terms of the Cartesian coordinates {{math|(x, y, z)}} by:

The surfaces of constant {{math|σ}} form confocal parabolic cylinders

that open towards {{math|+y}}, whereas the surfaces of constant {{math|τ}} form confocal parabolic cylinders

that open in the opposite direction, i.e., towards {{math|−y}}. The foci of all these parabolic cylinders are located along the line defined by {{math|x {{=}} y {{=}} 0}}. The radius {{math|r}} has a simple formula as well

that proves useful in solving the Hamilton–Jacobi equation in parabolic coordinates for the inverse-square central force problem of mechanics; for further details, see the Laplace–Runge–Lenz vector article.

Scale factors

The scale factors for the parabolic cylindrical coordinates {{math|σ}} and {{math|τ}} are:

Differential elements

The infinitesimal element of volume is

The differential displacement is given by:

The differential normal area is given by:

Del

Let {{math|f}} be a scalar field. The gradient is given by

The Laplacian is given by

Let {{math|A}} be a vector field of the form:

The divergence is given by

The curl is given by

Other differential operators can be expressed in the coordinates {{math|(σ, τ)}} by substituting the scale factors into the general formulae found in orthogonal coordinates.

Relationship to other coordinate systems

Relationship to cylindrical coordinates {{math|(ρ, φ, z)}}:

Parabolic unit vectors expressed in terms of Cartesian unit vectors:

Parabolic cylinder harmonics

Since all of the surfaces of constant {{math|σ}}, {{math|τ}} and {{math|z}} are conicoids, Laplace's equation is separable in parabolic cylindrical coordinates. Using the technique of the separation of variables, a separated solution to Laplace's equation may be written:

and Laplace's equation, divided by {{math|V}}, is written:

Since the {{math|Z}} equation is separate from the rest, we may write

where {{math|m}} is constant. {{math|Z(z)}} has the solution:

Substituting {{math|−m²}} for 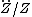, Laplace's equation may now be written:

We may now separate the {{math|S}} and {{math|T}} functions and introduce another constant {{math|n²}} to obtain:

The solutions to these equations are the parabolic cylinder functions

The parabolic cylinder harmonics for {{math|(m, n)}} are now the product of the solutions. The combination will reduce the number of constants and the general solution to Laplace's equation may be written:

Applications

The classic applications of parabolic cylindrical coordinates are in solving partial differential equations, e.g., Laplace's equation or the Helmholtz equation, for which such coordinates allow a separation of variables. A typical example would be the electric field surrounding a flat semi-infinite conducting plate.

Bibliography

{{cite book | author = Morse PM, Feshbach H | year = 1953 | title = Methods of Theoretical Physics, Part I | publisher = McGraw-Hill | location = New York | isbn = 0-07-043316-X|lccn=52011515 | page = 658}}
{{cite book | author = Margenau H, Murphy GM | year = 1956 | title = The Mathematics of Physics and Chemistry | publisher = D. van Nostrand | location = New York | pages = 186–187 | lccn = 55010911 }}
{{cite book | author = Korn GA, Korn TM |year = 1961 | title = Mathematical Handbook for Scientists and Engineers | publisher = McGraw-Hill | location = New York | id = ASIN B0000CKZX7 | page = 181 | lccn = 59014456}}
{{cite book | author = Sauer R, Szabó I | year = 1967 | title = Mathematische Hilfsmittel des Ingenieurs | publisher = Springer Verlag | location = New York | page = 96 | lccn = 67025285}}
{{cite book | author = Zwillinger D | year = 1992 | title = Handbook of Integration | publisher = Jones and Bartlett | location = Boston, MA | isbn = 0-86720-293-9 | page = 114}} Same as Morse & Feshbach (1953), substituting u_k for ξ_k.
{{cite book | author = Moon P, Spencer DE | year = 1988 | chapter = Parabolic-Cylinder Coordinates (μ, ν, z) | title = Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions | edition = corrected 2nd ed., 3rd print | publisher = Springer-Verlag | location = New York | pages = 21–24 (Table 1.04) | isbn = 978-0-387-18430-2}}

External links

MathWorld description of parabolic cylindrical coordinates

1 : Coordinate systems

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。