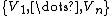“Parallelizable manifold”的意思、由来-开放百科全书

词条

Parallelizable manifold

释义

Examples
Remarks
See also
Notes
References

In mathematics, a differentiable manifold 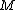of dimension n is called parallelizable^[1] if there exist smooth vector fields

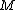on the manifold, such that at every point of the tangent vectors

provide a basis of the tangent space at . Equivalently, the tangent bundle is a trivial bundle,^[2] so that the associated principal bundle of linear frames has a global section on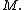

A particular choice of such a basis of vector fields on 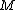is called a parallelization (or an absolute parallelism) of .

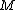Examples

An example with n = 1 is the circle: we can take V₁ to be the unit tangent vector field, say pointing in the anti-clockwise direction. The torus of dimension n is also parallelizable, as can be seen by expressing it as a cartesian product of circles. For example, take n = 2, and construct a torus from a square of graph paper with opposite edges glued together, to get an idea of the two tangent directions at each point. More generally, every Lie group G is parallelizable, since a basis for the tangent space at the identity element can be moved around by the action of the translation group of G on G (every translation is a diffeomorphism and therefore these translations induce linear isomorphisms between tangent spaces of points in G).
A classical problem was to determine which of the spheres Sⁿ are parallelizable. The zero-dimensional case S⁰ is trivially parallelizable. The case S¹ is the circle, which is parallelizable as has already been explained. The hairy ball theorem shows that S² is not parallelizable. However S³ is parallelizable, since it is the Lie group SU(2). The only other parallelizable sphere is S⁷; this was proved in 1958, by Michel Kervaire, and by Raoul Bott and John Milnor, in independent work. The parallelizable spheres correspond precisely to elements of unit norm in the normed division algebras of the real numbers, complex numbers, quaternions, and octonions, which allows one to construct a parallelism for each. Proving that other spheres are not parallelizable is more difficult, and requires algebraic topology.
The product of parallelizable manifolds is parallelizable.
Every orientable three-dimensional manifold is parallelizable.

Remarks

Any parallelizable manifold is orientable.
The term framed manifold (occasionally rigged manifold) is most usually applied to an embedded manifold with a given trivialisation of the normal bundle, and also for an abstract (i.e. non-embedded) manifold with a given stable trivialisation of the tangent bundle.

Notes

1. ^{{citation | last1=Bishop|first1=R.L.|last2=Goldberg|first2=S.I.|title=Tensor Analysis on Manifolds|year=1968|page=160}}
2. ^{{citation | last1=Milnor|first1=J.W.|last2=Stasheff|first2=J.D.|title=Characteristic Classes|year=1974|page=15}}

References

{{citation | last1=Bishop|first1=R.L.|author1-link=Richard L. Bishop|last2=Goldberg|first2=S.I. | title = Tensor Analysis on Manifolds| publisher=The Macmillan Company | year=1968|edition=First Dover 1980|isbn=0-486-64039-6}}
{{citation | last1=Milnor|first1=J.W.|author1-link=John Milnor|last2=Stasheff|first2=J.D. |author2-link=Jim Stasheff| title = Characteristic Classes| publisher=Princeton University Press | year=1974}}

4 : Differential topology|Fiber bundles|Vector bundles|Manifolds

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Examples

Remarks

See also

Notes

References