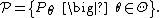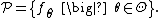- Definition
- Examples
- General remarks
- Comparisons with other classes of models
- See also
- Notes
- Bibliography
In statistics, a parametric model or parametric family or finite-dimensional model is a particular class of statistical models. Specifically, a parametric model is a family of probability distributions that has a finite number of parameters.
Definition
{{no footnotes|section|date=May 2012}}A statistical model is a collection of probability distributions on some sample space. We assume that the collection, {{math|𝒫}}, is indexed by some set {{math|Θ}}. For each {{math|θ ∈ Θ}}, let {{math|Pθ}} denote the corresponding member of the collection; so {{math|Pθ}} is a cumulative distribution function. Then a statistical model can be written as
The model is a parametric model if {{math|Θ ⊆ ℝk}} for some positive integer {{math|k}}.
When the model consists of absolutely continuous distributions, it is often specified in terms of corresponding probability density functions:
Examples
- The Poisson family of distributions is parametrized by a single number {{math|λ > 0}}:
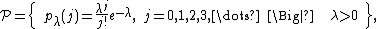
where {{math|pλ}} is the probability mass function. This family is an exponential family.
- The normal family is parametrized by {{math|θ {{=}} (μ, σ)}}, where {{math|μ ∈ ℝ}} is a location parameter and {{math|σ > 0}} is a scale parameter:
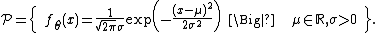
This parametrized family is both an exponential family and a location-scale family.
- The Weibull translation model has a three-dimensional parameter {{math|θ {{=}} (λ, β, μ)}}:
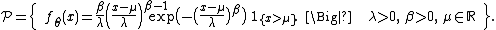
- The binomial model is parametrized by {{math|θ {{=}} (n, p)}}, where {{math|n}} is a non-negative integer and {{math|p}} is a probability (i.e. {{math|p ≥ 0}} and {{math|p ≤ 1}}):

This example illustrates the definition for a model with some discrete parameters.
General remarks
A parametric model is called identifiable if the mapping {{math|θ ↦ Pθ}} is invertible, i.e. there are no two different parameter values {{math|θ1}} and {{math|θ2}} such that {{math|Pθ1 {{=}} Pθ2}}.
Comparisons with other classes of models
Parametric models are contrasted with the semi-parametric, semi-nonparametric, and non-parametric models, all of which consist of an infinite set of "parameters" for description. The distinction between these four classes is as follows:{{Citation needed|date=October 2010}}
- in a "parametric" model all the parameters are in finite-dimensional parameter spaces;
- a model is "non-parametric" if all the parameters are in infinite-dimensional parameter spaces;
- a "semi-parametric" model contains finite-dimensional parameters of interest and infinite-dimensional nuisance parameters;
- a "semi-nonparametric" model has both finite-dimensional and infinite-dimensional unknown parameters of interest.
Some statisticians believe that the concepts "parametric", "non-parametric", and "semi-parametric" are ambiguous.[1] It can also be noted that the set of all probability measures has cardinality of continuum, and therefore it is possible to parametrize any model at all by a single number in (0,1) interval.[2] This difficulty can be avoided by considering only "smooth" parametric models.
See also
- Parametric family
- Parametric statistics
- Statistical model
- Statistical model specification
Notes
2. ^{{harvnb|Bickel|Klaassen| Ritov| Wellner| 1998|page=2}}
Bibliography
{{refbegin}}- {{citation
|author1-last = Bickel | author1-first = Peter J. | author1-link = Peter J. Bickel
|author2-last = Doksum | author2-first = Kjell A.
| title = Mathematical Statistics: Basic and selected topics
| volume = Volume 1
| edition = Second (updated printing 2007)
| year = 2001
| publisher = Prentice-Hall
- {{citation
| author1-last = Bickel | author1-first = Peter J. | author1-link = Peter J. Bickel
| author2-last = Klaassen | author2-first = Chris A. J.
| author3-last = Ritov | author3-first = Ya’acov
| author4-first = Jon A. | author4-last = Wellner
| year = 1998
| title= Efficient and Adaptive Estimation for Semiparametric Models
| publisher = Springer
- {{citation
| last = Davison
| first = A. C.
| title = Statistical Models
| publisher = Cambridge University Press
| year = 2003
- {{citation
| author-last = Le Cam | author-first = Lucien
| author-link = Lucien Le Cam
| author2-last = Yang | author2-first = Grace Lo | author2-link = Grace Yang
| title = Asymptotics in Statistics: Some basic concepts
| year = 2000
| publisher = Springer
- {{citation
| author1-last = Lehmann | author1-first = Erich L.
| author1-link = Erich Leo Lehmann
| author2-last = Casella | author2-first = George
| author2-link = George Casella
| title = Theory of Point Estimation
| edition = 2nd
| year = 1998
| publisher = Springer
- {{citation
| author1-last = Liese| author1-first = Friedrich
| author2-last = Miescke| author2-first = Klaus-J.
| title = Statistical Decision Theory: Estimation, testing, and selection
| year = 2008
| publisher = Springer
- {{citation
| title = Parametric Statistical Theory
| last1 = Pfanzagl
| first1 = Johann
| last2 = with the assistance of R. Hamböker
| year = 1994
| publisher = Walter de Gruyter
|MR=1291393}}{{refend}}{{DEFAULTSORT:Parametric Model}}
- Employee stock ownership plans
- Employee stocks
- Employee surveillance
- Employees Vote
- Employee training
- Employee Value
- Employer association
- Employer matching program
- Employer Matching Program
- Employer of Choice for Women
- Employers' liability act of 1880
- Employers' Liability (Compulsory Insurance) Act 1969
- Employer's Liability (Defective Equipment) Act 1969
- Employers of Poland
- Employers’ Liability (Compulsory Insurance) Act 1969
- Employing class
- Employment Abandoned
- Employment Act 2002
- Employment and Skills Group
- Employment and Social Insurance Act
- Employment and Training Act 1948
- Employment Authorization Card
- Employment Authorization Document
- Employment bureaus
- Employment by country