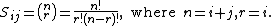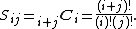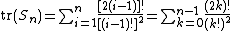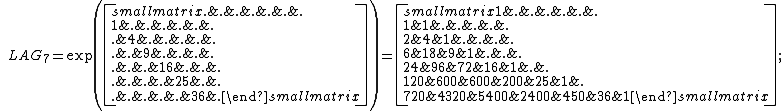- Construction
- Variants
- See also
- References
- External links
In mathematics, particularly matrix theory and combinatorics, the Pascal matrix is an infinite matrix containing the binomial coefficients as its elements. There are three ways to achieve this: as either an upper-triangular matrix, a lower-triangular matrix, or a symmetric matrix. The 5×5 truncations of these are shown below.
Upper triangular: 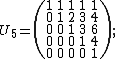
Lower triangular: 
Symmetric: 
These matrices have the pleasing relationship Sn = LnUn. From this it is easily seen that all three matrices have determinant 1, as the determinant of a triangular matrix is simply the product of its diagonal elements, which are all 1 for both Ln and Un. In other words, matrices Sn, Ln, and Un are unimodular, with Ln and Un having trace n.
The elements of the symmetric Pascal matrix are the binomial coefficients, i.e.
In other words,
Thus the trace of Sn is given by
with the first few terms given by the sequence 1, 3, 9, 29, 99, 351, 1275, … {{OEIS|A006134}}.
Construction
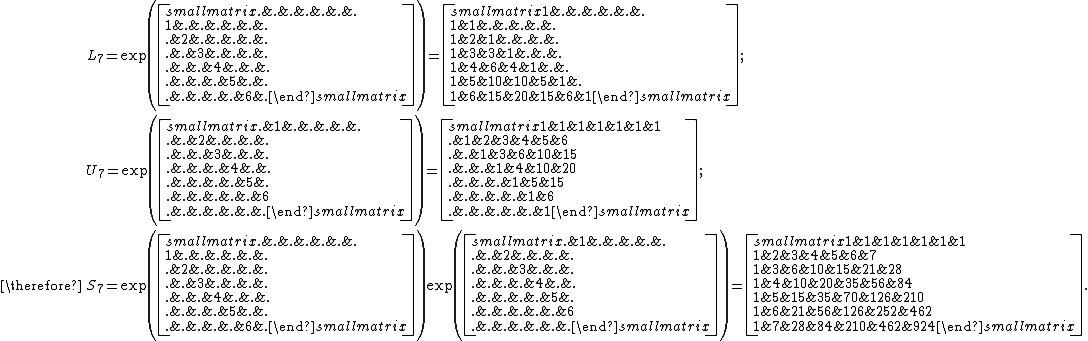
The Pascal matrix can actually be constructed by taking the matrix exponential of a special subdiagonal or superdiagonal matrix. The example below constructs a 7-by-7 Pascal matrix, but the method works for any desired n×n Pascal matrices. (Note that dots in the following matrices represent zero elements.)
It is important to note that one cannot simply assume exp(A)exp(B) = exp(A + B), for A and B n×n matrices. Such an identity only holds when AB = BA (i.e. when the matrices A and B commute). In the construction of symmetric Pascal matrices like that above, the sub- and superdiagonal matrices do not commute, so the (perhaps) tempting simplification involving the addition of the matrices cannot be made.
A useful property of the sub- and superdiagonal matrices used in the construction is that both are nilpotent; that is, when raised to a sufficiently high integer power, they degenerate into the zero matrix. (See shift matrix for further details.) As the n×n generalised shift matrices we are using become zero when raised to power n, when calculating the matrix exponential we need only consider the first n + 1 terms of the infinite series to obtain an exact result.
Variants
Interesting variants can be obtained by obvious modification of the matrix-logarithm PL7 and then application of the matrix exponential.
The first example below uses the squares of the values of the log-matrix and constructs a 7-by-7 "Laguerre"- matrix (or matrix of coefficients of Laguerre polynomials
The Laguerre-matrix is actually used with some other scaling and/or the scheme of alternating signs.
(Literature about generalizations to higher powers is not found yet)
The second example below uses the products v(v + 1) of the values of the log-matrix and constructs a 7-by-7 "Lah"- matrix (or matrix of coefficients of Lah numbers)
Using v(v − 1) instead provides a diagonal shifting to bottom-right.
The third example below uses the square of the original PL7-matrix, divided by 2, in other words: the first-order binomials (binomial(k, 2) ) in the second subdiagonal and constructs a matrix, which occurs in context of the derivatives and integrals of the Gaussian error function:
If this matrix is inverted (using, for instance, the negative matrix-logarithm), then this matrix has alternating signs and gives the coefficients of the derivatives (and by extension) the integrals of the Gauss' error-function . (Literature about generalizations to higher powers is not found yet.)
Another variant can be obtained by extending the original matrix to negative values:
See also
- Pascal's triangle
- LU decomposition
References
- G. S. Call and D. J. Velleman, "Pascal's matrices", American Mathematical Monthly, volume 100, (April 1993) pages 372–376
- {{Citation | first1 = Alan | last1 = Edelman | first2 = Gilbert | last2 = Strang | authorlink = Gilbert Strang | title = Pascal Matrices | journal = American Mathematical Monthly | volume = 111 | number = 3 | date = March 2004 | pages = 361–385 | url = http://mathdl.maa.org/images/upload_library/22/Ford/Edelman189-197.pdf | doi = 10.2307/4145127 | deadurl = yes | archiveurl = https://web.archive.org/web/20100704210817/http://mathdl.maa.org/images/upload_library/22/Ford/Edelman189-197.pdf | archivedate = 2010-07-04 | df = }}
External links
- G. Helms Pascalmatrix in a project of compilation of facts about Numbertheoretical matrices
- G. Helms Gauss-matrix
- Weisstein, Eric W. Gaussian-function
- Weisstein, Eric W. Erf-function
- Weisstein, Eric W. "Hermite Polynomial". Hermite-polynomials
- Endl, Kurt "Über eine ausgezeichnete Eigenschaft der Koeffizientenmatrizen des Laguerreschen und des Hermiteschen Polynomsystems". In: PERIODICAL VOLUME 65 Mathematische Zeitschrift Kurt Endl
- {{OEIS el|1=A066325|2=Coefficients of unitary Hermite polynomials Hen(x)|formalname=Coefficients of unitary Hermite polynomials He_n(x)}} (Related to Gauss-matrix).