“Path graph”的意思、由来-开放百科全书

词条

Path graph

释义

As Dynkin diagrams
See also
References
External links

{{about|a family of graphs|paths as parts of arbitrary graphs|Path (graph theory)}}{{distinguish|line graph}}{{infobox graph
| name = Path graph
| image =
| image_caption = A path graph on 6 vertices
| vertices = n
| edges = n − 1
| automorphisms = 2
| diameter = n − 1
| radius = ⌊n / 2⌋
| chromatic_number = 2
| chromatic_index = 2
| spectrum = {2 cos(k π / (n + 1)); k = 1, ..., n}
| properties = Unit distance
Bipartite graph
Tree
|notation =

}}

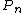
In the mathematical field of graph theory, a path graph or linear graph is a graph whose vertices can be listed in the order v₁, v₂, …, v_n such that the edges are {{nobreak|{v_i, v_i+1}}} where i = 1, 2, …, n − 1. Equivalently, a path with at least two vertices is connected and has two terminal vertices (vertices that have degree 1), while all others (if any) have degree 2.

Paths are often important in their role as subgraphs of other graphs, in which case they are called paths in that graph. A path is a particularly simple example of a tree, and in fact the paths are exactly the trees in which no vertex has degree 3 or more. A disjoint union of paths is called a linear forest.

Paths are fundamental concepts of graph theory, described in the introductory sections of most graph theory texts. See, for example, Bondy and Murty (1976), Gibbons (1985), or Diestel (2005).

As Dynkin diagrams

In algebra, path graphs appear as the Dynkin diagrams of type A. As such, they classify the root system of type A and the Weyl group of type A, which is the symmetric group.

References

{{cite book

|author = Bondy, J. A.; Murty, U. S. R.
|title = Graph Theory with Applications
|year = 1976
|publisher = North Holland
|isbn = 0-444-19451-7
|pages = 12–21
|url = http://www.ecp6.jussieu.fr/pageperso/bondy/books/gtwa/gtwa.html
|deadurl = yes
|archiveurl = https://web.archive.org/web/20100413104345/http://www.ecp6.jussieu.fr/pageperso/bondy/books/gtwa/gtwa.html
|archivedate = 2010-04-13
|df =
}}

{{cite book

| author = Diestel, Reinhard
| title = Graph Theory
| edition = 3rd
| url = http://www.math.uni-hamburg.de/home/diestel/books/graph.theory/
| publisher = Graduate Texts in Mathematics, vol. 173, Springer-Verlag
| year = 2005
| isbn = 3-540-26182-6
| pages = 6–9}}

External links

{{MathWorld | urlname=PathGraph | title=Path Graph }}

2 : Trees (graph theory)|Parametric families of graphs

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

As Dynkin diagrams

See also

References

External links