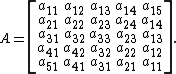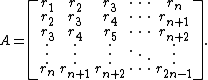“Persymmetric matrix”的意思、由来-开放百科全书

词条

Persymmetric matrix

释义

Definition 1
Definition 2
See also
References

In mathematics, persymmetric matrix may refer to:

a square matrix which is symmetric with respect to the northeast-to-southwest diagonal; or
a square matrix such that the values on each line perpendicular to the main diagonal are the same for a given line.

The first definition is the most common in the recent literature. The designation "Hankel matrix" is often used for matrices satisfying the property in the second definition.

Definition 1

Let A = (a_ij) be an n × n matrix. The first definition of persymmetric requires that

for all i, j.^[1]

For example, 5-by-5 persymmetric matrices are of the form

This can be equivalently expressed as AJ = JA^T where J is the exchange matrix.

A symmetric matrix is a matrix whose values are symmetric in the northwest-to-southeast diagonal. If a symmetric matrix is rotated by 90°, it becomes a persymmetric matrix. Symmetric persymmetric matrices are sometimes called bisymmetric matrices.

Definition 2

The second definition is due to Thomas Muir.^[2] It says that the square matrix A = (a_ij) is persymmetric if a_ij depends only on i + j. Persymmetric matrices in this sense, or Hankel matrices as they are often called, are of the form

A persymmetric determinant is the determinant of a persymmetric matrix.^[2]

A matrix for which the values on each line parallel to the main diagonal are constant, is called a Toeplitz matrix.

References

1. ^{{citation | first1=Gene H. | last1=Golub | author1-link=Gene H. Golub | first2=Charles F. | last2=Van Loan | author2-link=Charles F. Van Loan | year=1996 | title=Matrix Computations | edition=3rd | publisher=Johns Hopkins | place=Baltimore | isbn=978-0-8018-5414-9}}. See page 193.
2. ^¹{{Citation|last=Muir|first=Thomas|title=Treatise on the Theory of Determinants|page= 419|publisher= Dover Press|year= 1960}}

2 : Determinants|Matrices

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Definition 1

Definition 2

See also

References