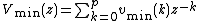“Pisarenko harmonic decomposition”的意思、由来-开放百科全书

词条

Pisarenko harmonic decomposition

释义

History
See also
References

Pisarenko harmonic decomposition, also referred to as Pisarenko's method, is a method of frequency estimation.^[1] This method assumes that a signal, , consists of complex exponentials in the presence of white noise. Because the number of complex exponentials must be known a priori, it is somewhat limited in its usefulness.

Pisarenko's method also assumes that 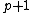values of the 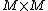autocorrelation matrix are either known or estimated. Hence, given the 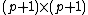autocorrelation matrix, the dimension of the noise subspace is equal to one and is spanned by the eigenvector corresponding to the minimum eigenvalue. This eigenvector is orthogonal to each of the signal vectors ^[2].

The frequency estimates may be determined by setting the frequencies equal to the angles of the roots of the eigenfilter

or the location of the peaks in the frequency estimation function

,

where 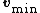is the noise eigenvector and

.

History

The method was first discovered in 1911 by Caratheodory, then rediscovered by Vladilen Fedorovich Pisarenko in 1973 while examining the problem of estimating the frequencies of complex signals in white noise. He found that the frequencies could be derived from the eigenvector corresponding to the minimum eigenvalue of the autocorrelation matrix.^[3]

References

1. ^Hayes, Monson H., Statistical Digital Signal Processing and Modeling, John Wiley & Sons, Inc., 1996. {{ISBN|0-471-59431-8}}.
2. ^Todd K. Moon, Wynn C. Stirling "Mathematical Methods and Algorithms for Signal Processing", 2000.
3. ^Pisarenko, V. F. The retrieval of harmonics from a covariance function Geophysics, J. Roy. Astron. Soc., vol. 33, pp. 347-366, 1973.

1 : Digital signal processing

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

History

See also

References