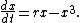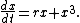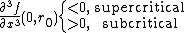“Pitchfork bifurcation”的意思、由来-开放百科全书

词条

Pitchfork bifurcation

释义

Supercritical case
Subcritical case
Formal definition
See also
References

In bifurcation theory, a field within mathematics, a pitchfork bifurcation is a particular type of local bifurcation where the system transitions from one fixed point to three fixed points. Pitchfork bifurcations, like Hopf bifurcations have two types – supercritical and subcritical.

In continuous dynamical systems described by ODEs—i.e. flows—pitchfork bifurcations occur generically in systems with symmetry.

Supercritical case

The normal form of the supercritical pitchfork bifurcation is

For negative values of , there is one stable equilibrium at . For there is an unstable equilibrium at , and two stable equilibria at .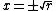

Subcritical case

The normal form for the subcritical case is

In this case, for 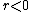the equilibrium at is stable, and there are two unstable equilibria at 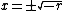. For the equilibrium at is unstable.

Formal definition

An ODE

described by a one parameter function 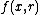with 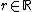satisfying:

(f is an odd function),

has a pitchfork bifurcation at 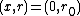. The form of the pitchfork is given

by the sign of the third derivative:

Note that subcritical and supercritical describe the stability of the outer lines of the pitchfork (dashed or solid, respectively) and are not dependent on which direction the pitchfork faces. For example, the negative of the first ODE above, 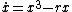, faces the same direction as the first picture but reverses the stability.

References

Steven Strogatz, Non-linear Dynamics and Chaos: With applications to Physics, Biology, Chemistry and Engineering, Perseus Books, 2000.
S. Wiggins, Introduction to Applied Nonlinear Dynamical Systems and Chaos, Springer-Verlag, 1990.

1 : Bifurcation theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Supercritical case

Subcritical case

Formal definition

See also

References