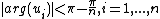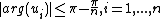- Spectra of
 -matrices
-matrices - Remarks
- See also
- Notes
- References
In mathematics, a  -matrix is a complex square matrix with every principal minor > 0. A closely related class is that of
-matrix is a complex square matrix with every principal minor > 0. A closely related class is that of  -matrices, which are the closure of the class of
-matrices, which are the closure of the class of  -matrices, with every principal minor
-matrices, with every principal minor  0.
0.
Spectra of  -matrices
-matrices
By a theorem of Kellogg,[1][2] the eigenvalues of  - and
- and  - matrices are bounded away from a wedge about the negative real axis as follows:
- matrices are bounded away from a wedge about the negative real axis as follows:
Ifare the eigenvalues of an
-dimensional
-matrix, where
, then
If,
,
are the eigenvalues of an
-dimensional
-matrix, then
Remarks
The class of nonsingular M-matrices is a subset of the class of  -matrices. More precisely, all matrices that are both
-matrices. More precisely, all matrices that are both  -matrices and Z-matrices are nonsingular
-matrices and Z-matrices are nonsingular 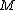 -matrices. The class of sufficient matrices is another generalization of
-matrices. The class of sufficient matrices is another generalization of  -matrices.[3]
-matrices.[3]
The linear complementarity problem 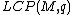 has a unique solution for every vector
has a unique solution for every vector  if and only if
if and only if 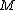 is a
is a  -matrix.[4]
-matrix.[4]
If the Jacobian of a function is a  -matrix, then the function is injective on any rectangular region of
-matrix, then the function is injective on any rectangular region of  .[5]
.[5]
A related class of interest, particularly with reference to stability, is that of 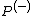 -matrices, sometimes also referred to as
-matrices, sometimes also referred to as  -matrices. A matrix
-matrices. A matrix  is a
is a 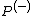 -matrix if and only if
-matrix if and only if 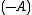 is a
is a  -matrix (similarly for
-matrix (similarly for  -matrices). Since
-matrices). Since 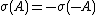 , the eigenvalues of these matrices are bounded away from the positive real axis.
, the eigenvalues of these matrices are bounded away from the positive real axis.
See also
- Hurwitz matrix
- Linear complementarity problem
- M-matrix
- Perron–Frobenius theorem
- Q-matrix
- Z-matrix (mathematics)
Notes
2. ^{{cite journal|last1=Fang|first1=Li|title=On the spectra of P- and P0-matrices|journal=Linear Algebra and its Applications|date=July 1989|volume=119|pages=1–25|doi=10.1016/0024-3795(89)90065-7}}
3. ^{{cite journal|first1=Zsolt|last1=Csizmadia|first2=Tibor|last2=Illés|title=New criss-cross type algorithms for linear complementarity problems with sufficient matrices|journal=Optimization Methods and Software|volume=21|year=2006|number=2|pages=247–266|doi=10.1080/10556780500095009|url=http://www.cs.elte.hu/opres/orr/download/ORR03_1.pdf|format=pdf |mr=2195759|}}
4. ^{{cite journal|last1=Murty|first1=Katta G.|title=On the number of solutions to the complementarity problem and spanning properties of complementary cones|journal=Linear Algebra and its Applications|date=January 1972|volume=5|issue=1|pages=65–108|doi=10.1016/0024-3795(72)90019-5}}
5. ^{{cite journal|last1=Gale|first1=David|last2=Nikaido|first2=Hukukane|title=The Jacobian matrix and global univalence of mappings|journal=Mathematische Annalen|date=10 December 2013|volume=159|issue=2|pages=81–93|doi=10.1007/BF01360282}}
References
- {{cite journal|first1=Zsolt|last1=Csizmadia|first2=Tibor|last2=Illés|title=New criss-cross type algorithms for linear complementarity problems with sufficient matrices|journal=Optimization Methods and Software|volume=21|year=2006|number=2|pages=247–266|doi=10.1080/10556780500095009|
url=http://www.cs.elte.hu/opres/orr/download/ORR03_1.pdf|format=pdf |mr=2195759|ref=harv}}
- David Gale and Hukukane Nikaido, The Jacobian matrix and global univalence of mappings, Math. Ann. 159:81-93 (1965) {{doi|10.1007/BF01360282}}
- Li Fang, On the Spectra of
 - and
- and  -Matrices, Linear Algebra and its Applications 119:1-25 (1989)
-Matrices, Linear Algebra and its Applications 119:1-25 (1989) - R. B. Kellogg, On complex eigenvalues of
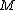 and
and  matrices, Numer. Math. 19:170-175 (1972)
matrices, Numer. Math. 19:170-175 (1972)
- Tougher Than Leather
- Tough Guys
- Tough justice
- Toughkenamon, PA
- Toughkenamon, Pennsylvania
- Tough Love with Mick Molloy
- Toughman Contest
- Toughman Contests
- Toughness
- Touhoku Broadcasting Company
- Touhou
- Touhou Party
- Touhou Project
- Toukai
- Toukijin
- Toukiou
- Toukizin
- Toukley
- Toukley, New South Wales
- Touko Laaksonen
- Toukyo
- Toukyou
- Toul
- Toulminville, Alabama
- Toulo de Graffenried