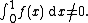1. Definitions
    Prevalence and shyness  Local prevalence and shyness 

2. Theorems involving prevalence and shyness

3. References

In mathematics, the notions of prevalence and shyness are notions of "almost everywhere" and "measure zero" that are well-suited to the study of infinite-dimensional spaces and make use of the translation-invariant Lebesgue measure on finite-dimensional real spaces. The term "shy" was suggested by the American mathematician John Milnor.

Definitions

Prevalence and shyness

Let V be a real topological vector space and let S be a Borel-measurable subset of V. S is said to be prevalent if there exists a finite-dimensional subspace P of V, called the probe set, such that for all v ∈ V we have v + p ∈ S for λ_P-almost all p ∈ P, where λ_P denotes the dim(P)-dimensional Lebesgue measure on P. Put another way, for every v ∈ V, Lebesgue-almost every point of the hyperplane v + P lies in S.

A non-Borel subset of V is said to be prevalent if it contains a prevalent Borel subset.

A Borel subset of V is said to be shy if its complement is prevalent; a non-Borel subset of V is said to be shy if it is contained within a shy Borel subset.

An alternative, and slightly more general, definition is to define a set S to be shy if there exists a transverse measure for S (other than the trivial measure).

Local prevalence and shyness

A subset S of V is said to be locally shy if every point v ∈ V has a neighbourhood N_v whose intersection with S is a shy set. S is said to be locally prevalent if its complement is locally shy.

Theorems involving prevalence and shyness

• If S is shy, then so is every subset of S and every translate of S.
• Every shy Borel set S admits a transverse measure that is finite and has compact support. Furthermore, this measure can be chosen so that its support has arbitrarily small diameter.
• Any finite or countable union of shy sets is also shy.
• Any shy set is also locally shy. If V is a separable space, then every locally shy subset of V is also shy.
• A subset S of n-dimensional Euclidean space Rⁿ is shy if and only if it has Lebesgue measure zero.
• Any prevalent subset S of V is dense in V.
• If V is infinite-dimensional, then every compact subset of V is shy.

In the following, "almost every" is taken to mean that the stated property holds of a prevalent subset of the space in question.

• Almost every continuous function from the interval [0, 1] into the real line R is nowhere differentiable; here the space V is C([0, 1]; R) with the topology induced by the supremum norm.
• Almost every function f in the L^p space L¹([0, 1]; R) has the property that

Clearly, the same property holds for the spaces of k-times differentiable functions C^k([0, 1]; R).

• For 1 < p ≤ +∞, almost every sequence a = (a_n)_n∈N in ℓ^p has the property that the series

diverges.

• Prevalence version of the Whitney embedding theorem: Let M be a compact manifold of class C¹ and dimension d contained in Rⁿ. For 1 ≤ k ≤ +∞, almost every C^k function f : Rⁿ → R^2d+1 is an embedding of M.
• If A is a compact subset of Rⁿ with Hausdorff dimension d, m ≥ d, and 1 ≤ k ≤ +∞, then, for almost every C^k function f : Rⁿ → R^m, f(A) also has Hausdorff dimension d.
• For 1 ≤ k ≤ +∞, almost every C^k function f : Rⁿ → Rⁿ has the property that all of its periodic points are hyperbolic. In particular, the same is true for all the period p points, for any integer p.

References

• {{cite journal

• {{cite journal

• Al Faw Palace
• Al-Faw Port
• Alfaya
• Alfaya (party)
• Alfa Yaya of Labe
• Al-Fayed
• Al-fayoum
• Al-Fayyum University
• Al Fayyūm Governorate
• Al-Fazl Al-Tubrusi
• Al Fazl Mosque
• Al Fazl (newspaper)
• Alfbad
• Alf Bakken
• Alf Barbagallo
• Alf Barber
• Alf Barbour
• Alfbard
• Alf (barque)
• Alf Barraclough
• Alf Bartlett
• Alf Basnett
• Alf Baud
• Alf Bauman
• Alf Bellis