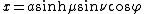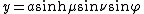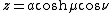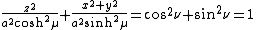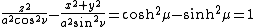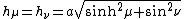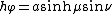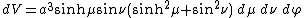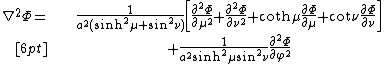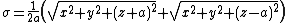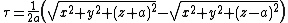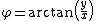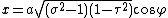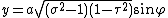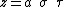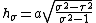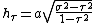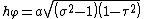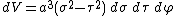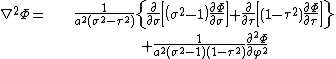“Prolate spheroidal coordinates”的意思、由来-开放百科全书

词条

Prolate spheroidal coordinates

释义

Definition
Scale factors
Alternative definition
Alternative scale factors
References
Bibliography
No angles convention Angle convention Unusual convention
External links

Prolate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional elliptic coordinate system about the focal axis of the ellipse, i.e., the symmetry axis on which the foci are located. Rotation about the other axis produces oblate spheroidal coordinates. Prolate spheroidal coordinates can also be considered as a limiting case of ellipsoidal coordinates in which the two smallest principal axes are equal in length.

Prolate spheroidal coordinates can be used to solve various partial differential equations in which the boundary conditions match its symmetry and shape, such as solving for a field produced by two centers, which are taken as the foci on the z-axis. One example is solving for the wavefunction of an electron moving in the electromagnetic field of two positively charged nuclei, as in the hydrogen molecular ion, H₂⁺. Another example is solving for the electric field generated by two small electrode tips. Other limiting cases include areas generated by a line segment (μ = 0) or a line with a missing segment (ν=0).

Definition

The most common definition of prolate spheroidal coordinates 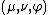is

where is a nonnegative real number and 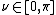. The azimuthal angle belongs to the interval .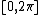

The trigonometric identity

shows that surfaces of constant form prolate spheroids, since they are ellipses rotated about the axis

joining their foci. Similarly, the hyperbolic trigonometric identity

shows that surfaces of constant form

hyperboloids of revolution.

The distances from the foci located at 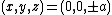are

Scale factors

The scale factors for the elliptic coordinates 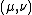are equal

whereas the azimuthal scale factor equals

Consequently, an infinitesimal volume element equals

and the Laplacian can be written

Other differential operators such as and 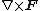can be expressed in the coordinates 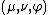by substituting the scale factors into the general formulae found in orthogonal coordinates.

Alternative definition

An alternative and geometrically intuitive set of prolate spheroidal coordinates 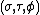are sometimes used,

where 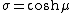and . Hence, the curves of constant are prolate spheroids, whereas the curves of constant are hyperboloids of revolution. The coordinate belongs to the interval [−1, 1], whereas the coordinate must be greater than or equal to one.

The coordinates and have a simple relation to the distances to the foci 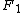and 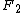. For any point in the plane, the sum 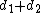of its distances to the foci equals 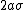, whereas their difference 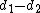equals 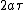. Thus, the distance to 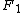is 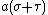, whereas the distance to 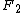is 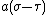. (Recall that 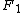and 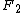are located at 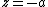and 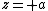, respectively.) This gives the following expressions for , , and :

Unlike the analogous oblate spheroidal coordinates, the prolate spheroid coordinates (σ, τ, φ) are not degenerate; in other words, there is a unique, reversible correspondence between them and the Cartesian coordinates

Alternative scale factors

The scale factors for the alternative elliptic coordinates 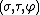are

while the azimuthal scale factor is now

Hence, the infinitesimal volume element becomes

and the Laplacian equals

Other differential operators such as and 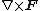can be expressed in the coordinates 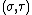by substituting the scale factors into the general formulae found in orthogonal coordinates.

As is the case with spherical coordinates, Laplace's equation may be solved by the method of separation of variables to yield solutions in the form of prolate spheroidal harmonics, which are convenient to use when boundary conditions are defined on a surface with a constant prolate spheroidal coordinate (See Smythe, 1968).

References

Bibliography

No angles convention

{{cite book |vauthors=Morse PM, Feshbach H | year = 1953 | title = Methods of Theoretical Physics, Part I | publisher = McGraw-Hill | location = New York | page = 661}} Uses ξ₁ = a cosh μ, ξ₂ = sin ν, and ξ₃ = cos φ.
{{cite book | author = Zwillinger D | year = 1992 | title = Handbook of Integration | publisher = Jones and Bartlett | location = Boston, MA | isbn = 0-86720-293-9 | page = 114}} Same as Morse & Feshbach (1953), substituting u_k for ξ_k.
{{cite book | last = Smythe | first = WR| title = Static and Dynamic Electricity |edition = 3rd | publisher = McGraw-Hill | location = New York | year = 1968}}
{{cite book |vauthors=Sauer R, Szabó I | year = 1967 | title = Mathematische Hilfsmittel des Ingenieurs | publisher = Springer Verlag | location = New York | page = 97 | lccn = 67025285}} Uses coordinates ξ = cosh μ, η = sin ν, and φ.

Angle convention

{{cite book |vauthors=Korn GA, Korn TM |year = 1961 | title = Mathematical Handbook for Scientists and Engineers | publisher = McGraw-Hill | location = New York | page = 177 | lccn = 59014456}} Korn and Korn use the (μ, ν, φ) coordinates, but also introduce the degenerate (σ, τ, φ) coordinates.
{{cite book |vauthors=Margenau H, Murphy GM | year = 1956 | title = The Mathematics of Physics and Chemistry | publisher = D. van Nostrand | location = New York| pages = 180–182 | lccn = 55010911 }} Similar to Korn and Korn (1961), but uses colatitude θ = 90° - ν instead of latitude ν.
{{cite book |vauthors=Moon PH, Spencer DE | year = 1988 | chapter = Prolate Spheroidal Coordinates (η, θ, ψ) | title = Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions | edition = corrected 2nd ed., 3rd print | publisher = Springer Verlag | location = New York | isbn = 0-387-02732-7 | pages = 28–30 (Table 1.06)}} Moon and Spencer use the colatitude convention θ = 90° − ν, and rename φ as ψ.

Unusual convention

{{cite book |vauthors=Landau LD, Lifshitz EM, Pitaevskii LP | year = 1984 | title = Electrodynamics of Continuous Media (Volume 8 of the Course of Theoretical Physics) | edition = 2nd | publisher = Pergamon Press | location = New York | isbn = 978-0-7506-2634-7 | pages = 19–29 }} Treats the prolate spheroidal coordinates as a limiting case of the general ellipsoidal coordinates. Uses (ξ, η, ζ) coordinates that have the units of distance squared.

External links

MathWorld description of prolate spheroidal coordinates

1 : Coordinate systems

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。