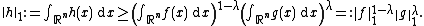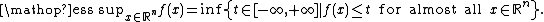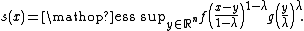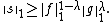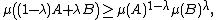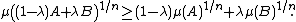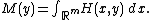- Statement of the inequality
- Essential form of the inequality
- Relationship to the Brunn–Minkowski inequality
- Applications in probability and statistics
- Notes
- References
In mathematics, the Prékopa–Leindler inequality is an integral inequality closely related to the reverse Young's inequality, the Brunn–Minkowski inequality and a number of other important and classical inequalities in analysis. The result is named after the Hungarian mathematicians András Prékopa and László Leindler.
Statement of the inequality
Let 0 < λ < 1 and let f, g, h : Rn → [0, +∞) be non-negative real-valued measurable functions defined on n-dimensional Euclidean space Rn. Suppose that these functions satisfy
{{NumBlk|:|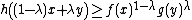 |{{EquationRef|1}}}}
|{{EquationRef|1}}}}for all x and y in Rn. Then
Essential form of the inequality
Recall that the essential supremum of a measurable function f : Rn → R is defined by
This notation allows the following essential form of the Prékopa–Leindler inequality: let 0 < λ < 1 and let f, g ∈ L1(Rn; [0, +∞)) be non-negative absolutely integrable functions. Let
Then s is measurable and
The essential supremum form was given in.[1] Its use can change the left side of the inequality. For example, a function g that takes the value 1 at exactly one point will not usually yield a zero left side in the "non-essential sup" form but it will always yield a zero left side in the "essential sup" form.
Relationship to the Brunn–Minkowski inequality
It can be shown that the usual Prékopa–Leindler inequality implies the Brunn–Minkowski inequality in the following form: if 0 < λ < 1 and A and B are bounded, measurable subsets of Rn such that the Minkowski sum (1 − λ)A + λB is also measurable, then
where μ denotes n-dimensional Lebesgue measure. Hence, the Prékopa–Leindler inequality can also be used[2] to prove the Brunn–Minkowski inequality in its more familiar form: if 0 < λ < 1 and A and B are non-empty, bounded, measurable subsets of Rn such that (1 − λ)A + λB is also measurable, then
Applications in probability and statistics
The Prékopa–Leindler inequality is useful in the theory of log-concave distributions, as it can be used to show that log-concavity is preserved by marginalization and independent summation of log-concave distributed random variables. Suppose that H(x,y) is a log-concave distribution for (x,y) ∈ Rm × Rn, so that by definition we have
{{NumBlk|:|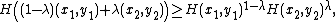 |{{EquationRef|2}}}}
|{{EquationRef|2}}}}and let M(y) denote the marginal distribution obtained by integrating over x:
Let y1, y2 ∈ Rn and 0 < λ < 1 be given. Then equation ({{EquationNote|2}}) satisfies condition ({{EquationNote|1}}) with h(x) = H(x,(1 − λ)y1 + λy2), f(x) = H(x,y1) and g(x) = H(x,y2), so the Prékopa–Leindler inequality applies. It can be written in terms of M as
which is the definition of log-concavity for M.
To see how this implies the preservation of log-convexity by independent sums, suppose that X and Y are independent random variables with log-concave distribution. Since the product of two log-concave functions is log-concave, the joint distribution of (X,Y) is also log-concave. Log-concavity is preserved by affine changes of coordinates, so the distribution of (X + Y, X − Y) is log-concave as well. Since the distribution of X+Y is a marginal over the joint distribution of (X + Y, X − Y), we conclude that X + Y has a log-concave distribution.
Notes
2. ^Gardner, Richard J. (2002). "The Brunn–Minkowski inequality". Bull. Amer. Math. Soc. (N.S.) 39 (3): pp. 355–405 (electronic). doi:10.1090/S0273-0979-02-00941-2. {{issn|0273-0979}}.
References
- {{cite journal
| last=Gardner
| first=Richard J.
| title=The Brunn–Minkowski inequality
| journal=Bull. Amer. Math. Soc. (N.S.)
| volume=39
| issue=3
| year=2002
| pages =355–405 (electronic)
| issn = 0273-0979
| url = http://www.ams.org/bull/2002-39-03/S0273-0979-02-00941-2/S0273-0979-02-00941-2.pdf
| doi=10.1090/S0273-0979-02-00941-2
}}
- {{ cite journal
| last=Prékopa
| first=András
| title=Logarithmic concave measures with application to stochastic programming
| journal=Acta Sci. Math.
| volume=32
| year=1971
| pages=301–316
| url=http://rutcor.rutgers.edu/~prekopa/SCIENT1.pdf
}}
- {{ cite journal
| last=Prékopa
| first=András
| title=On logarithmic concave measures and functions
| journal=Acta Sci. Math.
| volume=34
| year=1973
| pages=335–343
| url=http://rutcor.rutgers.edu/~prekopa/SCIENT2.pdf
}}{{DEFAULTSORT:Prekopa-Leindler Inequality}}
- Staatliche Ingenieurschule Wolfenbüttel
- Staatliche Kunsthalle
- Staatliche Kunsthalle Karlsruhe
- Staatliche Museen zu Berlin
- Staatliche Museum Schwerin
- Staatliche Sammlung fuer Agyptische Kunst
- Staatliche Sammlung fur Agyptische Kunst
- Staatliches Bauhaus
- Staatliches Filmarchiv der DDR
- Staatliches Hofbrauhaus in München
- Staatliches Landschulheim Marquartstein
- Staatliches Lindenau Museum
- Staatliches Museum fuer Tierkunde Dresden
- Staatliches Museum fur Tierkunde Dresden
- Staatliches Museum für Naturkunde Stuttgart
- Staatliches Museum für Tierkunde Dresden
- Staatliches Museum für Völkerkunde München
- Staatliches Museum Schwerin
- Staatlich Fachingen
- Staatsanwaltschaft
- Staatsballett Berlin
- Staatsbibliothek (disambiguation)
- Staatsburg, NY
- Staatscourant
- Staats-Eisenbahn-Gesellschaft