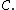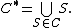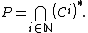“Pseudo-arc”的意思、由来-开放百科全书

词条

Pseudo-arc

释义

History
Construction
Chains Pseudo-arc
References

In general topology, the pseudo-arc is the simplest nondegenerate hereditarily indecomposable continuum. The pseudo-arc is an arc-like homogeneous continuum. R.H. Bing proved that, in a certain well-defined sense, most continua in Rⁿ, n ≥ 2, are homeomorphic to the pseudo-arc.

History

In 1920, Bronisław Knaster and Kazimierz Kuratowski asked whether a nondegenerate homogeneous continuum in the Euclidean plane R² must be a Jordan curve. In 1921, Stefan Mazurkiewicz asked whether a nondegenerate continuum in R² that is homeomorphic to each of its nondegenerate subcontinua must be an arc. In 1922, Knaster discovered the first example of a hereditarily indecomposable continuum K, later named the pseudo-arc, giving a negative answer to a Mazurkiewicz question. In 1948, R.H. Bing proved that Knaster's continuum is homogeneous, i.e. for any two of its points there is a homeomorphism taking one to the other. Yet also in 1948, Edwin Moise showed that Knaster's continuum is homeomorphic to each of its non-degenerate subcontinua. Due to its resemblance to the fundamental property of the arc, namely, being homeomorphic to all its nondegenerate subcontinua, Moise called his example M a pseudo-arc.{{efn|George W. Henderson later showed that a decomposable continuum homeomorphic to all its nondegenerate subcontinua must be an arc.{{sfn|Henderson|1960}}}} Bing's construction is a modification of Moise's construction of M, which he had first heard described in a lecture. In 1951, Bing proved that all hereditarily indecomposable arc-like continua are homeomorphic — this implies that Knaster's K, Moise's M, and Bing's B are all homeomorphic. Bing also proved that the pseudo-arc is typical among the continua in a Euclidean space of dimension at least 2 or an infinite-dimensional separable Hilbert space.{{efn|The history of the discovery of the pseudo-arc is described in ,{{sfn|Nadler|1992}} pp 228–229.}}

Construction

The following construction of the pseudo-arc follows {{harv|Wayne Lewis|1999}}.

Chains

At the heart of the definition of the pseudo-arc is the concept of a chain, which is defined as follows:

A chain is a finite collection of open sets in a metric space such that if and only if The elements of a chain are called its links, and a chain is called an ε-chain if each of its links has diameter less than ε.

While being the simplest of the type of spaces listed above, the pseudo-arc is actually very complex. The concept of a chain being crooked (defined below) is what endows the pseudo-arc with its complexity. Informally, it requires a chain to follow a certain recursive zig-zag pattern in another chain. To 'move' from the mth link of the larger chain to the nth, the smaller chain must first move in a crooked manner from the mth link to the (n-1)th link, then in a crooked manner to the (m+1)th link, and then finally to the nth link.

More formally:

Let and be chains such that

each link of is a subset of a link of , and
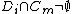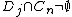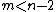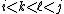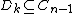for any indices i, j, m, and n with , , and , there exist indices and with (or ) and and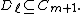

Then is crooked in

Pseudo-arc

For any collection C of sets, let 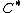denote the union of all of the elements of C. That is, let

The pseudo-arc is defined as follows:

Let p and q be distinct points in the plane and be a sequence of chains in the plane such that for each i,

the first link of 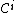contains p and the last link contains q,
the chain 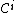is a 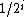-chain,
the closure of each link of 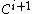is a subset of some link of 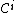, and
the chain 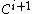is crooked in .

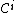Let

Then P is a pseudo-arc.

References

Notes{{notelist|notes=}}Citations

Bibliography{{refbegin}}

R.H. Bing, A homogeneous indecomposable plane continuum, Duke Math. J., 15:3 (1948), 729–742
R.H. Bing, Concerning hereditarily indecomposable continua, Pacific J. Math., 1 (1951), 43–51
{{cite journal |last=Henderson |first=George W. |title=Proof that every compact decomposable continuum which is topologically equivalent to each of its nondegenerate subcontinua is an arc |journal=Annals of Mathematics |volume=72 |year=1960 |pages=421–428 |ref=harv}}
Trevor Irwin and Sławomir Solecki, Projective Fraïssé limits and the pseudo-arc, Trans. AMS, 358:7 (2006), 3077-3096.
Bronisław Knaster, Un continu dont tout sous-continu est indécomposable. Fundamenta Mathematicae 3 (1922): pp. 247–286
Wayne Lewis, The Pseudo-Arc, Bol. Soc. Mat. Mexicana, 5 (1999), 25–77.
Wayne Lewis and Piotr Minc, Drawing the pseudo-arc, Houston J. Math. 36 (2010), 905-934.
Edwin Moise, An indecomposable plane continuum which is homeomorphic to each of its nondegenerate subcontinua, Trans. Amer. Math. Soc., 63, no. 3 (1948), 581–594
{{cite book| first=Sam B., Jr| last=Nadler| title=Continuum theory. An introduction.| series=Pure and Applied Mathematics| publisher=Marcel Dekker| year=1992| place=New York| isbn=0-8247-8659-9| ref=harv}}

1 : Continuum theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。