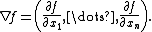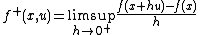1. Formal definition

2. Properties

3. Generalization to nondifferentiable functions

4. Related notions

5. See also

6. Notes

7. References

In convex analysis and the calculus of variations, branches of mathematics, a pseudoconvex function is a function that behaves like a convex function with respect to finding its local minima, but need not actually be convex. Informally, a differentiable function is pseudoconvex if it is increasing in any direction where it has a positive directional derivative.

Formal definition

Formally, a real-valued differentiable function ƒ defined on a (nonempty) convex open set X in the finite-dimensional Euclidean space Rⁿ is said to be pseudoconvex if, for all {{nowrap|x, y ∈ X}} such that 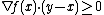, we have .^[1] Here ∇ƒ is the gradient of ƒ, defined by

Properties

Every convex function is pseudoconvex, but the converse is not true. For example, the function {{nowrap|ƒ(x) {{=}} x + x³}} is pseudoconvex but not convex. Any pseudoconvex function is quasiconvex, but the converse is not true since the function {{nowrap|ƒ(x) {{=}} x³}} is quasiconvex but not pseudoconvex. Pseudoconvexity is primarily of interest because a point x* is a local minimum of a pseudoconvex function ƒ if and only if it is a stationary point of ƒ, which is to say that the gradient of ƒ vanishes at x*:

^[2]

Generalization to nondifferentiable functions

The notion of pseudoconvexity can be generalized to nondifferentiable functions as follows.^[3] Given any function {{nowrap|ƒ : X → R}} we can define the upper Dini derivative of ƒ by

where u is any unit vector. The function is said to be pseudoconvex if it is increasing in any direction where the upper Dini derivative is positive. More precisely, this is characterized in terms of the subdifferential ∂ƒ as follows:

• For all {{nowrap|x, y ∈ X}}, if there exists an {{nowrap|x ∈ ∂ƒ(x)}} such that 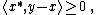then {{nowrap|ƒ(x) ≤ ƒ(z)}} for all z on the line segment adjoining x and y.

Related notions

A {{visible anchor|pseudoconcave function}} is a function whose negative is pseudoconvex. A {{visible anchor|pseudolinear function}} is a function that is both pseudoconvex and pseudoconcave.^[4] For example, linear–fractional programs have pseudolinear objective functions and linear–inequality constraints: These properties allow fractional–linear problems to be solved by a variant of the simplex algorithm (of George B. Dantzig).^[5][6][7]

See also

• Pseudoconvexity
• Convex function
• Quasiconvex function

Notes

References

• {{citation|first1=Christodoulos A.|last1=Floudas|first2=Panos M.|last2=Pardalos|title=Encyclopedia of Optimization|chapter=Generalized monotone multivalued maps|publisher=Springer|year=2001|isbn=978-0-7923-6932-5|page=227}}.
• {{cite journal|ref=harv|title=Pseudo-Convex Functions|journal=Journal of the Society for Industrial and Applied Mathematics Series A Control|volume=3|issue=2|pages=281–290 |date=January 1965|doi=10.1137/0303020|first=O. L.|last=Mangasarian|issn=0363-0129}}.
• {{cite journal|ref=harv|first=T.|last=Rapcsak|title=On pseudolinear functions|journal=European Journal of Operational Research|volume=50|issue=3|date=1991-02-15|pages=353–360|issn=0377-2217|doi=10.1016/0377-2217(91)90267-Y}}

• Ashtu
• Ash (typical Persian food)
• Ashuapmushan River
• Ashuapmushaun River
• Ashuelot
• Ashuelot Covered Bridge
• Ashuelot, New Hampshire
• Ashuelot, NH
• Ashuelot pond
• Ashuganj Upazila
• Ashugh
• A. Shulman
• As Hundred
• Ash United FC
• Ash United F. C.
• Ash United F C
• A. S. Hunt
• Ashura (2005 film)
• Ashu Rabo
• Ashura day
• Ashur-ahha-iddina
• Ashura (holiday)
• Ashurajo No Hitomi
• Ashurajo no Hitomi
• Ashurajou no Hitomi