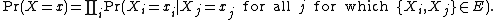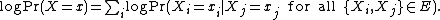“Pseudolikelihood”的意思、由来-开放百科全书

词条

Pseudolikelihood

释义

Definition
Properties
References

{{disputed|date=October 2016}}In statistical theory, a pseudolikelihood is an approximation to the joint probability distribution of a collection of random variables. The practical use of this is that it can provide an approximation to the likelihood function of a set of observed data which may either provide a computationally simpler problem for estimation, or may provide a way of obtaining explicit estimates of model parameters.

The pseudolikelihood approach was introduced by Julian Besag^[1] in the context of analysing data having spatial dependence.

Definition

Given a set of random variables 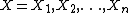and a set of dependencies between these random variables, where 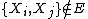implies is conditionally independent of given 's neighbors, the pseudolikelihood of 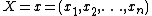is

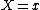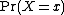Here is a vector of variables, is a vector of values. The expression above means that each variable in the vector has a corresponding value in the vector . The expression is the probability that the vector of variables has values equal to the vector . Because situations can often be described using state variables ranging over a set of possible values, the expression 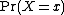can therefore represent the probability of a certain state among all possible states allowed by the state variables.

The pseudo-log-likelihood is a similar measure derived from the above expression. Thus

One use of the pseudolikelihood measure is as an approximation for inference about a Markov or Bayesian network, as the pseudolikelihood of an assignment to may often be computed more efficiently than the likelihood, particularly when the latter may require marginalization over a large number of variables.

Properties

Use of the pseudolikelihood in place of the true likelihood function in a maximum likelihood analysis can lead to good estimates, but a straightforward application of the usual likelihood techniques to derive information about estimation uncertainty, or for significance testing, would in general be incorrect.^[2]

References

1. ^{{citation |author=Besag, J. |year=1975 |title=Statistical Analysis of Non-Lattice Data |journal=The Statistician |volume=24 |issue=3 |pages=179–195 |jstor=2987782}}
2. ^Dodge, Y. (2003) The Oxford Dictionary of Statistical Terms, Oxford University Press. {{isbn|0-19-920613-9}} {{full citation needed|date=March 2017}}

1 : Statistical inference

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。