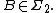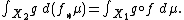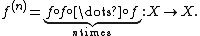“Pushforward measure”的意思、由来-开放百科全书

词条

Pushforward measure

释义

Definition
Main property: change-of-variables formula
Examples and applications
A generalization
See also
Notes
References

In measure theory, a discipline within mathematics, a pushforward measure (also push forward, push-forward or image measure) is obtained by transferring ("pushing forward") a measure from one measurable space to another using a measurable function.

Definition

Given measurable spaces 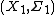and , a measurable mapping 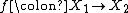and a measure 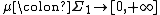, the pushforward of is defined to be the measure 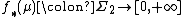given by

for

This definition applies mutatis mutandis for a signed or complex measure.

The pushforward measure is also denoted as 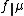, , 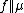or .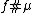

Main property: change-of-variables formula

Theorem:^[1] A measurable function g on X₂ is integrable with respect to the pushforward measure f_∗(μ) if and only if the composition is integrable with respect to the measure μ. In that case, the integrals coincide, i.e.,

Examples and applications

A natural "Lebesgue measure" on the unit circle S¹ (here thought of as a subset of the complex plane C) may be defined using a push-forward construction and Lebesgue measure λ on the real line R. Let λ also denote the restriction of Lebesgue measure to the interval [0, 2π) and let f : [0, 2π) → S¹ be the natural bijection defined by f(t) = exp(i t). The natural "Lebesgue measure" on S¹ is then the push-forward measure f_∗(λ). The measure f_∗(λ) might also be called "arc length measure" or "angle measure", since the f_∗(λ)-measure of an arc in S¹ is precisely its arc length (or, equivalently, the angle that it subtends at the centre of the circle.)
The previous example extends nicely to give a natural "Lebesgue measure" on the n-dimensional torus Tⁿ. The previous example is a special case, since S¹ = T¹. This Lebesgue measure on Tⁿ is, up to normalization, the Haar measure for the compact, connected Lie group Tⁿ.
Gaussian measures on infinite-dimensional vector spaces are defined using the push-forward and the standard Gaussian measure on the real line: a Borel measure γ on a separable Banach space X is called Gaussian if the push-forward of γ by any non-zero linear functional in the continuous dual space to X is a Gaussian measure on R.
Consider a measurable function f : X → X and the composition of f with itself n times:

This iterated function forms a dynamical system. It is often of interest in the study of such systems to find a measure μ on X that the map f leaves unchanged, a so-called invariant measure, one for which f_∗(μ) = μ.

One can also consider quasi-invariant measures for such a dynamical system: a measure μ on X is called quasi-invariant under f if the push-forward of μ by f is merely equivalent to the original measure μ, not necessarily equal to it.

Many natural probability distributions, such as the chi distribution, can be obtained via this construction.

A generalization

In general, any measurable function can be pushed forward, the push-forward then becomes a linear operator, known as the transfer operator or Frobenius–Perron operator. In finite-dimensional spaces this operator typically satisfies the requirements of the Frobenius–Perron theorem, and the maximal eigenvalue of the operator corresponds to the invariant measure.

The adjoint to the push-forward is the pullback; as an operator on spaces of functions on measurable spaces, it is the composition operator or Koopman operator.

Notes

1. ^Sections 3.6–3.7 in {{Harvnb|Bogachev}}

References

{{Citation

| last = Bogachev
| first = Vladimir I.
| title = Measure Theory
| place = Berlin
| publisher = Springer Verlag
| year = 2007
| pages =
| url =
| doi =
| zbl =
| isbn = 9783540345138}}

{{Citation

| last = Teschl
| first = Gerald
| authorlink=Gerald Teschl
| title = Topics in Real and Functional Analysis
| place =
| publisher =
| year = 2015
| pages =
| url = http://www.mat.univie.ac.at/~gerald/ftp/book-fa/index.html
| doi =
| zbl =
| isbn = }}{{DEFAULTSORT:Pushforward Measure}}

1 : Measures (measure theory)

随便看