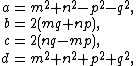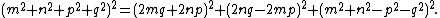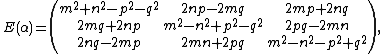- Parametrization of primitive quadruples
- Alternate parametrization
- Properties
- Relationship with quaternions and rational orthogonal matrices
- Primitive Pythagorean quadruples with small norm
- See also
- References
- External links
A Pythagorean quadruple is a tuple of integers {{math|a}}, {{math|b}}, {{math|c}} and {{math|d}}, such that {{math|a{{sup|2}} + b{{sup|2}} + c{{sup|2}} {{=}} d{{sup|2}}}}. They are solutions of a Diophantine equation and often only positive integer values are considered.[1] However, to provide a more complete geometric interpretation, the integer values can be allowed to be negative and zero (thus allowing Pythagorean triples to be included) with the only condition being that {{math|d > 0}}. In this setting, a Pythagorean quadruple {{math|(a, b, c, d)}} defines a cuboid with integer side lengths {{math|{{abs|a}}}}, {{math|{{abs|b}}}}, and {{math|{{abs|c}}}}, whose space diagonal has integer length {{math|d}}. Pythagorean quadruples, with this interpretation are thus also called Pythagorean boxes.[2] In this article we will assume, unless otherwise stated, that the values of a Pythagorean quadruple are all positive integers.
Parametrization of primitive quadruples
A Pythagorean quadruple is called primitive if the greatest common divisor of its entries is 1. Every Pythagorean quadruple is an integer multiple of a primitive quadruple. The set of primitive Pythagorean quadruples for which {{math|a}} is odd can be generated by the formulas
where {{math|m}}, {{math|n}}, {{math|p}}, {{math|q}} are non-negative integers with greatest common divisor 1 such that {{math|m + n + p + q}} is odd.[3][4][1] Thus, all primitive Pythagorean quadruples are characterized by Lebesgue's identity{{clarify|Is there a source for this name?|date=June 2017}}
Alternate parametrization
All Pythagorean quadruples (including non-primitives, and with repetition, though {{math|a}}, {{math|b}} and {{math|c}} do not appear in all possible orders) can be generated from two positive integers {{math|a}} and {{math|b}} as follows:
If {{math|a}} and {{math|b}} have different parity, let {{math|p}} be any factor of {{math|a{{sup|2}} + b{{sup|2}}}} such that {{math|p{{sup|2}} < a{{sup|2}} + b{{sup|2}}}}. Then {{math|c {{=}} {{sfrac|a{{sup|2}} + b{{sup|2}} − p{{sup|2}}|2p}}}} and {{math|d {{=}} {{sfrac|a{{sup|2}} + b{{sup|2}} + p{{sup|2}}|2p}}}}. Note that {{math|p {{=}} d − c}}.
A similar method exists[5] for generating all Pythagorean quadruples for which {{math|a}} and {{math|b}} are both even. Let {{math|l {{=}} {{sfrac|a|2}}}} and {{math|m {{=}} {{sfrac|b|2}}}} and let {{math|n}} be a factor of {{math|l{{sup|2}} + m{{sup|2}}}} such that {{math|n{{sup|2}} < l{{sup|2}} + m{{sup|2}}}}. Then {{math|c {{=}} {{sfrac|l{{sup|2}} + m{{sup|2}} − n{{sup|2}}|n}}}} and {{math|d {{=}} {{sfrac|l{{sup|2}} + m{{sup|2}} + n{{sup|2}}|n}}}}. This method generates all Pythagorean quadruples exactly once each when {{math|l}} and {{math|m}} run through all pairs of natural numbers and {{math|n}} runs through all permissible values for each pair.
No such method exists if both {{math|a}} and {{math|b}} are odd, in which case no solutions exist as can be seen by the parametrization in the previous section.
Properties
The largest number that always divides the product {{math|abcd}} is 12.[6] The quadruple with the minimal product is (1, 2, 2, 3).
Relationship with quaternions and rational orthogonal matrices
A primitive Pythagorean quadruple {{math|(a, b, c, d)}} parametrized by {{math|(m,n,p,q)}} corresponds to the first column of the matrix representation {{math|E(α)}} of conjugation {{math|α(⋅){{overline|α}}}} by the Hurwitz quaternion {{math|α {{=}} m + ni + pj + qk}} restricted to the subspace of {{math|ℍ}} spanned by {{math|i}}, {{math|j}}, {{math|k}}, which is given by
where the columns are pairwise orthogonal and each has norm {{math|d}}. Furthermore, we have {{math|{{sfrac|1|d}}E(α) ∈ SO(3,ℚ)}}, and, in fact, all 3 × 3 orthogonal matrices with rational coefficients arise in this manner.[7]
Primitive Pythagorean quadruples with small norm
There are 31 primitive Pythagorean quadruples in which all entries are less than 30.
| ( | 1 | , | 2 | , | 2 | , | 3 | ) | ( | 2 | , | 10 | , | 11 | , | 15 | ) | ( | 4 | , | 13 | , | 16 | , | 21 | ) | ( | 2 | , | 10 | , | 25 | , | 27 | ) |
| ( | 2 | , | 3 | , | 6 | , | 7 | ) | ( | 1 | , | 12 | , | 12 | , | 17 | ) | ( | 8 | , | 11 | , | 16 | , | 21 | ) | ( | 2 | , | 14 | , | 23 | , | 27 | ) |
| ( | 1 | , | 4 | , | 8 | , | 9 | ) | ( | 8 | , | 9 | , | 12 | , | 17 | ) | ( | 3 | , | 6 | , | 22 | , | 23 | ) | ( | 7 | , | 14 | , | 22 | , | 27 | ) |
| ( | 4 | , | 4 | , | 7 | , | 9 | ) | ( | 1 | , | 6 | , | 18 | , | 19 | ) | ( | 3 | , | 14 | , | 18 | , | 23 | ) | ( | 10 | , | 10 | , | 23 | , | 27 | ) |
| ( | 2 | , | 6 | , | 9 | , | 11 | ) | ( | 6 | , | 6 | , | 17 | , | 19 | ) | ( | 6 | , | 13 | , | 18 | , | 23 | ) | ( | 3 | , | 16 | , | 24 | , | 29 | ) |
| ( | 6 | , | 6 | , | 7 | , | 11 | ) | ( | 6 | , | 10 | , | 15 | , | 19 | ) | ( | 9 | , | 12 | , | 20 | , | 25 | ) | ( | 11 | , | 12 | , | 24 | , | 29 | ) |
| ( | 3 | , | 4 | , | 12 | , | 13 | ) | ( | 4 | , | 5 | , | 20 | , | 21 | ) | ( | 12 | , | 15 | , | 16 | , | 25 | ) | ( | 12 | , | 16 | , | 21 | , | 29 | ) |
| ( | 2 | , | 5 | , | 14 | , | 15 | ) | ( | 4 | , | 8 | , | 19 | , | 21 | ) | ( | 2 | , | 7 | , | 26 | , | 27 | ) |
See also
- Beal's conjecture
- Euler brick
- Euler's sum of powers conjecture
- Fermat cubic
- Jacobi–Madden equation
- Prouhet–Tarry–Escott problem
- Quaternions and spatial rotation
- Euler-Rodrigues formula for 3D rotations
- Taxicab number
References
2. ^R.A. Beauregard and E. R. Suryanarayan, Pythagorean boxes, Math. Magazine 74 (2001), 222–227.
3. ^R.D. Carmichael, Diophantine Analysis, New York: John Wiley & Sons, 1915.
4. ^L.E. Dickson, Some relations between the theory of numbers and other branches of mathematics, in Villat (Henri), ed., Conférence générale, Comptes rendus du Congrès international des mathématiciens, Strasbourg, Toulouse, 1921, pp. 41–56; reprint Nendeln/Liechtenstein: Kraus Reprint Limited, 1967; Collected Works 2, pp. 579–594.
5. ^Sierpiński, Wacław, Pythagorean Triangles, Dover, 2003 (orig. 1962), p.102–103.
6. ^MacHale, Des, and van den Bosch, Christian, "Generalising a result about Pythagorean triples", Mathematical Gazette 96, March 2012, pp. 91-96.
7. ^J. Cremona, Letter to the Editor, Amer. Math. Monthly 94 (1987), 757–758.
External links
- {{MathWorld|urlname=PythagoreanQuadruple|title=Pythagorean Quadruple}}
- {{MathWorld|urlname=LebesgueIdentity|title=Lebesgue's Identity}}
- Zimmerius albigularis
- Zimmerius cinereicapillus
- Zimmerius flavidifrons
- Zimmerli
- Zimmerli art museum
- Zimmerli Museum
- Zimmerman Field
- Zimmerman House
- Zimmerman House (Horseheads, New York)
- Zimmerman House (Manchester, New Hampshire)
- Zimmerman Island
- Zimmerman Kame
- Zimmerman-Laband syndrome
- Zimmerman Looking Back
- Zimmermannia heringiella
- Zimmermannia (moth)
- Zimmermanniella
- Zimmermann-Laband syndrome
- Zimmermann, Pierre
- Zimmermann (publisher)
- Zimmerman, Ontario
- Zimmerman-Rudeen House
- Zimmerman's
- Zimmerman's, California
- Zimmerman Site