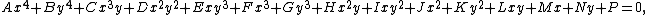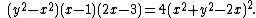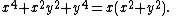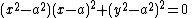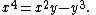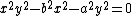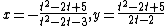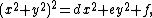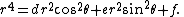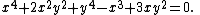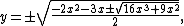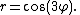“Quartic plane curve”的意思、由来-开放百科全书

词条

Quartic plane curve

释义

Examples
Ampersand curve Bean curve Bicuspid curve Bow curve Cruciform curve Spiric section Three-leaved clover
References

A quartic plane curve is a plane algebraic curve of the fourth degree. It can be defined by a bivariate quartic equation:

with at least one of A, B, C, D, E not equal to zero. This equation has 15 constants. However, it can be multiplied by any non-zero constant without changing the curve; thus by the choice of an appropriate constant of multiplication, any one of the coefficients can be set to 1, leaving only 14 constants. Therefore, the space of quartic curves can be identified with the real projective space 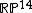. It also follows, from Cramer's theorem on algebraic curves, that there is exactly one quartic curve that passes through a set of 14 distinct points in general position, since a quartic has 14 degrees of freedom.

A quartic curve can have a maximum of:

Four connected components
Twenty-eight bi-tangents
Three ordinary double points.

One may also consider quartic curves over other fields (or even rings), for instance the complex numbers. In this way, one gets Riemann surfaces, which are one-dimensional objects over C, but are two-dimensional over R. An example is the Klein quartic. Additionally, one can look at curves in the projective plane, given by homogeneous polynomials.

Examples

{{multiple image
|direction=vertical
|align=right
|width=130
|image1=Ampersandcurve.svg
|caption1=Ampersand curve
|image2=Bean curve.svg
|caption2=Bean curve
|image3=Bicuspid curve.svg
|caption3=Bicuspid curve
|image4=Bowcurve.svg
|caption4=Bow curve
|image5=Cruciform1.png
|caption5=Cruciform curve with parameters (b,a) being (1,1) in red; (2,2) in green; (3,3) in blue.
|image6=Cruciform2.png
|caption6=Cruciform curve with parameters (b,a) being (1,1) in red; (2,1) in green; (3,1) in blue.
|image7=Spiric section.svg
|caption7=Spiric section
|image8=Three-leaved clover.svg
|caption8=Three-leaved clover in Cartesian coordinates
|image9=Three-leaved clover polar.svg
|caption9=Three-leaved clover in polar coordinates
}}

Various combinations of coefficients in the above equation give rise to various important families of curves as listed below.

Bicorn
Bullet-nose curve
Cartesian oval
Cassini oval
Deltoid curve
Hippopede
Kampyle of Eudoxus
Klein quartic

Lemniscate
- Lemniscate of Bernoulli
- Lemniscate of Gerono
Limaçon
Lüroth quartic
Spiric section
Squircle
- Lamé's special quartic
Toric section
Trott curve

Ampersand curve

The ampersand curve is a quartic plane curve given by the equation:

It has genus zero, with three ordinary double points, all in the real plane.

^[1]

Bean curve

The bean curve is a quartic plane curve with the equation:

The bean curve has genus zero. It has one singularity at the origin, an ordinary triple point.

^[2]^[3]

Bicuspid curve

The bicuspid is a quartic plane curve with the equation

where a determines the size of the curve.

The bicuspid has only the two nodes as singularities, and hence is a curve of genus one.

^[4]

Bow curve

The bow curve is a quartic plane curve with the equation:

The bow curve has a single triple point at x=0, y=0, and consequently is a rational curve, with genus zero.

^[5]

Cruciform curve

The cruciform curve, or cross curve is a quartic plane curve given by the equation

where a and b are two parameters determining the shape of the curve.

The cruciform curve is related by a standard quadratic transformation, x ↦ 1/x, y ↦ 1/y to the ellipse a²x² + b²y² = 1, and is therefore a rational plane algebraic curve of genus zero. The cruciform curve has three double points in the real projective plane, at x=0 and y=0, x=0 and z=0, and y=0 and z=0.

^[6]

Because the curve is rational, it can be parametrized by rational functions. For instance, if a=1 and b=2, then

parametrizes the points on the curve outside of the exceptional cases where a denominator is zero.

Spiric section

Spiric sections can be defined as bicircular quartic curves that are symmetric with respect to the x and y axes. Spiric sections are included in the family of toric sections and include the family of hippopedes and the family of Cassini ovals. The name is from σπειρα meaning torus in ancient Greek.

The Cartesian equation can be written as

and the equation in polar coordinates as

Three-leaved clover

The three-leaved clover is the quartic plane curve

By solving for y, the curve can be described by the following function:

where the two appearances of ± are independent of each other, giving up to four distinct values of y for each x.

The parametric equation of three-leaved clover is

^[7]

In polar coordinates (x = r cos φ, y = r sin φ) the equation is

It is a special case of rose curve with k = 3.

This curve has a triple point at the origin (0, 0) and has three double tangents.

References

1. ^{{MathWorld|title=Ampersand Curve|urlname=AmpersandCurve}}
2. ^{{Citation | last1=Cundy | first1=H. Martyn | last2=Rollett | first2=A. P. | title=Mathematical models | origyear=1952 | publisher=Clarendon Press, Oxford | edition=2nd | isbn=978-0-906212-20-2 | mr=0124167 | year=1961 | page=72}}
3. ^ {{MathWorld|title=Bean Curve|urlname=BeanCurve}}
4. ^{{MathWorld|title=Bicuspid Curve|urlname=BicuspidCurve}}
5. ^{{MathWorld|title=Bow|urlname=Bow}}
6. ^{{MathWorld|title=Cruciform curve|urlname=Cruciform}}
7. ^Gibson, C. G., Elementary Geometry of Algebraic Curves, an Undergraduate Introduction, Cambridge University Press, Cambridge, 2001, {{isbn|978-0-521-64641-3}}. Pages 12 and 78.

1 : Algebraic curves

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。