“Quasi-finite field”的意思、由来-开放百科全书

词条

Quasi-finite field

释义

Formal definition
Examples
Notes
References

In mathematics, a quasi-finite field^[1] is a generalisation of a finite field. Standard local class field theory usually deals with complete valued fields whose residue field is finite (i.e. non-archimedean local fields), but the theory applies equally well when the residue field is only assumed quasi-finite.^[2]

Formal definition

A quasi-finite field is a perfect field K together with an isomorphism of topological groups

where K_s is an algebraic closure of K (necessarily separable because K is perfect). The field extension K_s/K is infinite, and the Galois group is accordingly given the Krull topology. The group 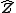is the profinite completion of integers with respect to its subgroups of finite index.

This definition is equivalent to saying that K has a unique (necessarily cyclic) extension K_n of degree n for each integer n ≥ 1, and that the union of these extensions is equal to K_s.^[3] Moreover, as part of the structure of the quasi-finite field, there is a generator F_n for each Gal(K_n/K), and the generators must be coherent, in the sense that if n divides m, the restriction of F_m to K_n is equal to F_n.

Examples

The most basic example, which motivates the definition, is the finite field K = GF(q). It has a unique cyclic extension of degree n, namely K_n = GF(qⁿ). The union of the K_n is the algebraic closure K_s. We take F_n to be the Frobenius element; that is, F_n(x) = x^q.

Another example is K = C((T)), the ring of formal Laurent series in T over the field C of complex numbers. (These are simply formal power series in which we also allow finitely many terms of negative degree.) Then K has a unique cyclic extension

of degree n for each n ≥ 1, whose union is an algebraic closure of K called the field of Puiseux series, and that a generator of Gal(K_n/K) is given by

This construction works if C is replaced by any algebraically closed field C of characteristic zero.^[4]

Notes

1. ^{{harv|Artin|Tate|2009|loc=§XI.3}} say that the field satisfies "Moriya's axiom"
2. ^As shown by Mikao Moriya {{harv|Serre|1979|loc=chapter XIII, p. 188}}
3. ^{{harv|Serre|1979|loc=§XIII.2 exercise 1, p. 192}}
4. ^{{harv|Serre|1979|loc=§XIII.2, p. 191}}

References

{{Citation

| last=Artin
| first=Emil
| author-link=Emil Artin
| last2=Tate
| first2=John
| author2-link=John Tate
| title=Class field theory
| publisher=American Mathematical Society
| year=2009
| origyear=1967
| isbn=978-0-8218-4426-7
| mr=2467155 | zbl=1179.11040
}}

{{citation | last=Serre | first=Jean-Pierre | authorlink=Jean-Pierre Serre | title=Local Fields |translator-last1=Greenberg|translator-first=Marvin Jay|translator-link1=Marvin Greenberg | series=Graduate Texts in Mathematics | volume=67 | publisher=Springer-Verlag | year=1979 | isbn=0-387-90424-7 | zbl=0423.12016 | mr=554237 }}

2 : Class field theory|Field theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。