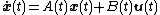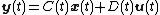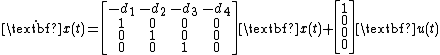“Realization (systems)”的意思、由来-开放百科全书

词条

Realization (systems)

释义

LTI System
Canonical realizations
General System
D = 0
System identification
See also
References

In systems theory, a realization of a state space model is an implementation of a given input-output behavior. That is, given an input-output relationship, a realization is a quadruple of (time-varying) matrices 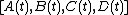such that

with 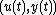describing the input and output of the system at time .

LTI System

For a linear time-invariant system specified by a transfer matrix, , a realization is any quadruple of matrices 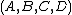such that .

Canonical realizations

Any given transfer function which is strictly proper can easily be transferred into state-space by the following approach (this example is for a 4-dimensional, single-input, single-output system)):

Given a transfer function, expand it to reveal all coefficients in both the numerator and denominator. This should result in the following form:

.

The coefficients can now be inserted directly into the state-space model by the following approach:

.

This state-space realization is called controllable canonical form (also known as phase variable canonical form) because the resulting model is guaranteed to be controllable (i.e., because the control enters a chain of integrators, it has the ability to move every state).

The transfer function coefficients can also be used to construct another type of canonical form

.

This state-space realization is called observable canonical form because the resulting model is guaranteed to be observable (i.e., because the output exits from a chain of integrators, every state has an effect on the output).

General System

D = 0

If we have an input , an output , and a weighting pattern 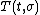then a realization is any triple of matrices 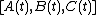such that 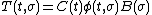where is the state-transition matrix associated with the realization.^[1]

System identification

System identification techniques take the experimental data from a system and output a realization. Such techniques can utilize both input and output data (e.g. eigensystem realization algorithm) or can only include the output data (e.g. frequency domain decomposition). Typically an input-output technique would be more accurate, but the input data is not always available.

References

1. ^{{cite book|first=Roger W.|last=Brockett|title=Finite Dimensional Linear Systems|publisher=John Wiley & Sons|year=1970|isbn=978-0-471-10585-5}}

2 : Models of computation|Systems theory

随便看