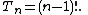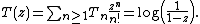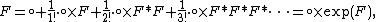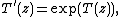“Recursive tree”的意思、由来-开放百科全书

词条

Recursive tree

释义

Properties
Bijections
Applications
References

In graph theory, a recursive tree (i.e., unordered tree) is a non-planar labeled rooted tree. A size-n recursive tree is labeled by distinct integers 1, 2, ..., n, where the labels are strictly increasing starting at the root labeled 1. Recursive trees are non-planar, which means that the children of a particular node are not ordered. E.g. the following two size-three recursive trees are the same.

       1          1      / \\   =    / \\     /   \\      /   \\    2     3    3     2

Recursive trees also appear in literature under the name Increasing Cayley trees.

Properties

The number of size-n recursive trees is given by

Hence the exponential generating function T(z) of the sequence T_n is given by

Combinatorically a recursive tree can be interpreted as a root followed by an unordered sequence of recursive trees. Let F denote the family of recursive trees.

where denotes the node labeled by 1, × the Cartesian product and the partition product for labeled objects.

By translation of the formal description one obtains the differential equation for T(z)

with T(0) = 0.

Bijections

There are bijective correspondences between recursive trees of size n and permutations of size n − 1.

Applications

Recursive trees can be generated using a simple stochastic process. Such random recursive trees are used as simple models for epidemics.

References

Analytic Combinatorics, Philippe Flajolet and Robert Sedgewick, Cambridge University Press, 2008
Varieties of Increasing Trees, Francois Bergeron, Philippe Flajolet, and Bruno Salvy. In Proceedings of the 17th Colloquium on Trees in Algebra and Programming, Rennes, France, February 1992. Proceedings published in Lecture Notes in Computer Science vol. 581, J.-C. Raoult Ed., 1992, pp. 24–48.
Profile of random trees: correlation and width of random recursive trees and binary search trees Michael Drmota and Hsien-Kuei Hwang, Adv. Appl. Prob., 37, 1-21, 2005.
Profiles of random trees: Limit theorems for random recursive trees and binary search trees, Michael Fuchs, Hsien-Kuei Hwang, Ralph Neininger., Algorithmica, 46:3-4, 2006, 367-407, 2006.

1 : Trees (graph theory)

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。