突变论tubianlun

描述突变现象的一般理论。对任何一个系统，其状态的变化可以分为两种类型，一种是连续的渐变，如牛顿力学中常提到的匀加速直线运动，另一种是不连续的、跳跃式的突变，如一定质量的气体在一定的温度和压力之下会变成液体，地壳的剧烈运动引起地震等等。以往我们处理问题的数学工具基本上是以微积分为基础的，系统的状态通常满足一组微分方程，由于微分方程的解必须是可微分的函数，所以它适合于描述连续的渐变的过程，对丰富多彩的突变现象就显得无能为力。60年代末法国数学家托姆(Thom)在当时奇点理论（数学的一个分支）发展的最新成就基础上提出了突变理论，从数学上对各种各样的突变现象进行了分类。突变论强调从整体上把握系统的性质，为研究系统的突变行为提供了新的思路。它处理问题的一般过程如下：❶确定刻划系统宏观状态的变量(x₁,x₂，…，xn)，这些变量应反映系统所表现出来的宏观性质。
❷确定影响系统行为的控制参数(u₁,u₂，…，ur)。
❸系统的行为受某个依赖于(x₁,x₂，…，xn;u₁,u₂，…，ur)的函数P(x₁,x₂，…，xn;u₁,u₂，…，ur)所支配，在突变论中，这个函数称为势函数。
❹考察势函数的性质，就能够确定系统突变可能发生的范围。由于现实世界中的突变现象千姿百态。因此一般说来所谓的势函数可以非常复杂。但是托姆突变论的关于基本突变的分类定理指出，对于两个变量的系统尽管势函数P千千万万，但只要势函数中控制参量的个数r（称为余维）不超过4，那么突变方式在某种意义上只有7个基本类型，其它势函数通过变换可以化为这7种形式。下面就是这7种突变类型的名称，控制参量的个数r和一般的势函数的形式。

名称	余维r (控制 参量个 数)	函数形式
折叠型 尖点形 燕尾型 双曲脐点型 椭隧脐点型 蝴蝶型 抛物脐点型	1 2 3 3 3 4 4	x31+u1x1 x41+u1x21+u2x1 x51+u1x31+u2x21+u3x1 x31+x32+u1x1x2+u2x1+u3x2 x31-x1x22+u1(x21+x22)+u2x1+u3x2 x61+u1x41+u2x31+u3x21+u4x1 x21x2+x42+u1x21+u2x22+u3x1+u4x2

对于双变量系统只要控制参量的个数不超过4，我们就可以把决定系统状态的势函数化成上面7种类型之一，从而可以决定系统的行为曲面。如尖点型突变，它所对应的行为曲面如下图所示。假定系统的状态在外界参数的控制下从Q0向Q₁移动，到达悬崖边缘后，系统的状态就会掉到下半曲面的Q₂点上，这也就是系统状态的突变现象。

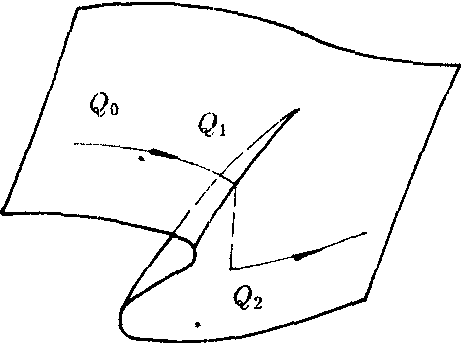
自从突变论在60年代末问世以来，其应用已遍及自然科学和社会科学各领域。总的来说，突变论的应用分为两类，一类是在力学、物理学等领域中的硬应用。另一类是在生物学、社会科学领域中的软应用，它使得我们可以讨论神经冲动传播、物种的兴衰、经济危机、战争爆发等各种突变行为。但像一切新理论的诞生发展一样，突变论（特别是它的应用）还须在实践中检验。修正与发展。