“Ribbon knot”的意思、由来-开放百科全书

词条

Ribbon knot

释义

Morse-theoretic formulation
Slice-ribbon conjecture
References

In the mathematical area of knot theory, a ribbon knot is a knot that bounds a self-intersecting disk with only ribbon singularities. Intuitively, this kind of singularity can be formed by cutting a slit in the disk and passing another part of the disk through the slit. More formally, this type of singularity is a self-intersection along an arc; the preimage of this arc consists of two arcs in the disc, one completely in the interior of the disk and the other having its two endpoints on the disk boundary.

Morse-theoretic formulation

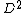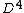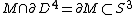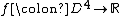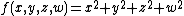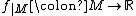A slice disc M is a smoothly embedded in with . Consider the function given by . By a small isotopy of M one can ensure that f restricts to a Morse function on M. One says is a ribbon knot if has no interior local maxima.

Slice-ribbon conjecture

Every ribbon knot is known to be a slice knot. A famous open problem, posed by Ralph Fox and known as the slice-ribbon conjecture, asks if the converse is true: is every slice knot ribbon?

{{harvtxt|Lisca|2007}} showed that the conjecture is true for knots of bridge number two. {{harvtxt|Greene|Jabuka|2011}} showed it to be true for three-strand pretzel knots. However, {{harvtxt|Gompf|Scharlemann|Thompson|2010}} suggested that the conjecture might not be true, and provided a family of knots that could be counterexamples to it.

References

{{citation

| last = Fox | first = R. H. | authorlink = Ralph Fox
| contribution = Some problems in knot theory
| location = Englewood Cliffs, N.J.
| mr = 0140100
| pages = 168–176
| publisher = Prentice-Hall
| title = Topology of 3-manifolds and related topics (Proc. The Univ. of Georgia Institute, 1961)
| year = 1962}}. Reprinted by Dover Books, 2010.

{{citation

| last1 = Gompf | first1 = Robert E. | author1-link = Robert Gompf
| last2 = Scharlemann | first2 = Martin | author2-link = Martin Scharlemann
| last3 = Thompson | first3 = Abigail | author3-link = Abigail Thompson
| doi = 10.2140/gt.2010.14.2305
| issue = 4
| journal = Geometry & Topology
| mr = 2740649
| pages = 2305–2347
| title = Fibered knots and potential counterexamples to the property 2R and slice-ribbon conjectures
| volume = 14
| year = 2010| arxiv = 1103.1601}}.

{{citation

| last1 = Greene | first1 = Joshua
| last2 = Jabuka | first2 = Stanislav
| arxiv = 0706.3398
| doi = 10.1353/ajm.2011.0022
| issue = 3
| journal = American Journal of Mathematics
| mr = 2808326
| pages = 555–580
| title = The slice-ribbon conjecture for 3-stranded pretzel knots
| volume = 133
| year = 2011}}.

{{citation

| last = Kauffman | first = Louis H. | authorlink = Louis Kauffman
| isbn = 0-691-08434-3
| location = Princeton, NJ
| mr = 907872
| publisher = Princeton University Press
| series = Annals of Mathematics Studies
| title = On Knots
| volume = 115
| year = 1987}}.

{{citation

| last = Lisca | first = Paolo
| doi = 10.2140/gt.2007.11.429
| journal = Geometry & Topology
| mr = 2302495
| pages = 429–472
| title = Lens spaces, rational balls and the ribbon conjecture
| volume = 11
| year = 2007| arxiv = math/0701610{{Knot theory|state=collapsed}}

2 : Knots and links|Slice knots and links

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。