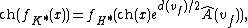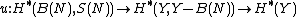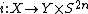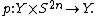“Riemann–Roch theorem for smooth manifolds”的意思、由来-开放百科全书

词条

Riemann–Roch theorem for smooth manifolds

释义

Formulation
Corollaries
Notes

In mathematics, a Riemann–Roch theorem for smooth manifolds is a version of results such as the Hirzebruch–Riemann–Roch theorem or Grothendieck–Riemann–Roch theorem (GRR) without a hypothesis making the smooth manifolds involved carry a complex structure. Results of this kind were obtained by Michael Atiyah and Friedrich Hirzebruch in 1959, reducing the requirements to something like a spin structure.

Formulation

Let X and Y be oriented smooth closed manifolds,

and f: X → Y a continuous map.

Let v_f=f^*(TY) − TX in the K-group

K(X).

If dim(X) ≡ dim(Y) mod 2, then

where ch is the Chern character, d(v_f) an element of

the integral cohomology group H²(Y, Z) satisfying

d(v_f) ≡ f^* w₂(TY)-w₂(TX) mod 2,

f_K* the Gysin homomorphism for K-theory,

and f_H* the Gysin homomorphism for cohomology

.^[1]

This theorem was first proven by Atiyah and Hirzebruch.^[2]

The theorem is proven by considering several special cases.^[3]

If Y is the Thom space of a vector bundle V over X,

then the Gysin maps are just the Thom isomorphism.

Then, using the splitting principle, it suffices to check the theorem via explicit computation for line

bundles.

If f: X → Y is an embedding, then the

Thom space of the normal bundle of X in Y can be viewed as a tubular neighborhood of X

in Y, and excision gives a map

and

.

The Gysin map for K-theory/cohomology is defined to be the composition of the Thom isomorphism with these maps.

Since the theorem holds for the map from X to the Thom space of N,

and since the Chern character commutes with u and v, the theorem is also true for embeddings.

f: X → Y.

Finally, we can factor a general map f: X → Y

into an embedding

and the projection

The theorem is true for the embedding.

The Gysin map for the projection is the Bott-periodicity isomorphism, which commutes with the Chern character,

so the theorem holds in this general case also.

Corollaries

Atiyah and Hirzebruch then specialised and refined in the case X = a point, where the condition becomes the existence of a spin structure on Y. Corollaries are on Pontryagin classes and the J-homomorphism.

Notes

1. ^M. Karoubi, K-theory, an introduction, Springer-Verlag, Berlin (1978)
2. ^M. Atiyah and F. Hirzebruch, Riemann–Roch theorems for differentiable manifolds (Bull. Amer. Math. Soc. 65 (1959) 276–281)
3. ^M. Karoubi, K-theory, an introduction, Springer-Verlag, Berlin (1978)

3 : Theorems in differential geometry|Algebraic surfaces|Bernhard Riemann

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。