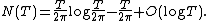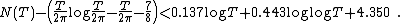“Riemann–von Mangoldt formula”的意思、由来-开放百科全书

词条

Riemann–von Mangoldt formula

释义

References

In mathematics, the Riemann–von Mangoldt formula, named for Bernhard Riemann and Hans Carl Friedrich von Mangoldt, describes the distribution of the zeros of the Riemann zeta function.

The formula states that the number N(T) of zeros of the zeta function with imaginary part greater than 0 and less than or equal to T satisfies

The formula was stated by Riemann in his notable paper "On the Number of Primes Less Than a Given Magnitude" (1859) and was finally proved by Mangoldt in 1905.

Backlund gives an explicit form of the error for all T greater than 2:

References

{{cite book | last=Edwards | first=H.M. | authorlink=Harold Edwards (mathematician) | title=Riemann's zeta function | series=Pure and Applied Mathematics | volume=58 | location=New York-London |publisher=Academic Press | year=1974 | isbn=0-12-232750-0 | zbl=0315.10035 }}
{{cite book | last=Ivić | first=Aleksandar | title=The theory of Hardy's Z-function | series=Cambridge Tracts in Mathematics | volume=196 | location=Cambridge | publisher=Cambridge University Press | year=2013 | isbn=978-1-107-02883-8 | zbl=1269.11075}}
{{cite book | last=Patterson | first=S.J. | title=An introduction to the theory of the Riemann zeta-function | series=Cambridge Studies in Advanced Mathematics | volume=14 | location=Cambridge | publisher=Cambridge University Press | year=1988 | isbn=0-521-33535-3 | zbl=0641.10029 }}

2 : Theorems in analytic number theory|Bernhard Riemann

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。