“Rosenbrock function”的意思、由来-开放百科全书

In mathematical optimization, the Rosenbrock function is a non-convex function, introduced by Howard H. Rosenbrock in 1960, which is used as a performance test problem for optimization algorithms.^[1] It is also known as Rosenbrock's valley or Rosenbrock's banana function.

The global minimum is inside a long, narrow, parabolic shaped flat valley. To find the valley is trivial. To converge to the global minimum, however, is difficult.

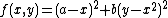
It has a global minimum at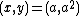

, where

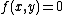. Usually these parameters are set such that

and

. Only in the trivial case where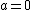

is the function symmetric and the minimum at the origin.

Multidimensional generalisations

One is the sum of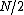

uncoupled 2D Rosenbrock problems, and is defined only for even

has exactly one minimum for

(at

) and exactly two minima for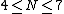

—the global minimum of all ones and a local minimum near

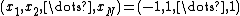. This result is obtained by setting the gradient of the function equal to zero, noticing that the resulting equation is a rational function of

. For small

the polynomials can be determined exactly and Sturm's theorem can be used to determine the number of real roots, while the roots can be bounded in the region of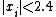

.^[5] For larger

this method breaks down due to the size of the coefficients involved.

Stationary points

Many of the stationary points of the function exhibit a regular pattern when plotted.^[5] This structure can be exploited to locate them.

Optimization examples

The Rosenbrock function can be efficiently optimized by adapting appropriate coordinate system without using any gradient information and without building local approximation models (in contrast to many derivate-free optimizers). The following figure illustrates an example of 2-dimensional Rosenbrock function optimization by

adaptive coordinate descent from starting point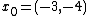

. The solution with the function value

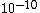can be found after 325 function evaluations.

Using the Nelder–Mead method from starting point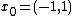

with a regular initial simplex a minimum is found with function value

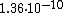after 185 function evaluations. The figure below visualizes the evolution of the algorithm.

References

1. ^{{cite journal|last=Rosenbrock|first=H.H.|title=An automatic method for finding the greatest or least value of a function|journal=The Computer Journal|year=1960|volume=3|issue=3|pages=175–184|doi=10.1093/comjnl/3.3.175| issn=0010-4620 }}
2. ^{{cite book|last=Simionescu|first=P.A.|title=Computer Aided Graphing and Simulation Tools for AutoCAD users|year=2014|publisher=CRC Press|location=Boca Raton, FL|isbn=978-1-4822-5290-3|edition=1st}}
3. ^{{cite journal |first=L. C. W. |last=Dixon |first2=D. J. |last2=Mills |title=Effect of Rounding Errors on the Variable Metric Method |journal=Journal of Optimization Theory and Applications |volume=80 |issue= |pages=175–179 |year=1994 |url=http://portal.acm.org/citation.cfm?id=179711 |doi=10.1007/BF02196600 }}
4. ^{{cite web |url = http://docs.scipy.org/doc/scipy-0.14.0/reference/tutorial/optimize.html#unconstrained-minimization-of-multivariate-scalar-functions-minimize|title = Generalized Rosenbrock's function|accessdate = 2008-09-16|website = |publisher = |date = }}
5. ^¹{{cite journal |first=Schalk |last=Kok |first2=Carl |last2=Sandrock |title=Locating and Characterizing the Stationary Points of the Extended Rosenbrock Function |journal=Evolutionary Computation |volume=17 |issue= 3|pages=437–53 |year=2009 |doi=10.1162/evco.2009.17.3.437 |pmid=19708775 }}

Multidimensional generalisations

Stationary points

Optimization examples

References

External links